Short Answer Type
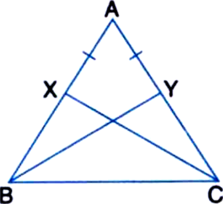
Given: X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY.
To Prove: XC = YB
Proof: In ∆ABC,
∵ AB = AC    | Given
∴ ∠ABC = ∠ACB    ...(1)
| Angles opposite to equal sides of a triangle are equal
Again, AB = AC Â Â Â | Given
AX = AY Â Â Â | Given
Subtracting, we get,
AB - AX = AC - AY
⇒    BX = CY    ...(2)
In ∆BXC and ∆CYB,
BX = CY Â Â Â | From (2)
BC = CB Â Â Â | Common
∠XBC = ∠YCB    | From (1)
∴ ∆BXC ≅ ∆CYB
| SAS congruence rule
∴ XC = YB    | CPCT
Long Answer Type In figure, ABCD is a square and ∠DEC is an equilateral triangle. Prove that
(i)   ∆ADE ≅ ∆BCE
(ii) Â Â Â AE = BE
(iii)  ∠DAE = 15°
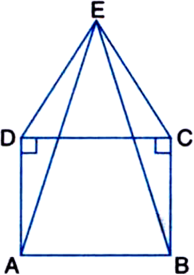
Short Answer Type
Switch
