 Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type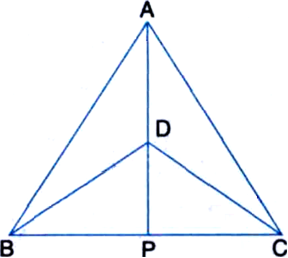
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
 Short Answer Type
Short Answer TypeAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of triangle PQR (see figure). Show that:
(i) ∆ABM ≅ ∆PQN
(ii) ∆ABC ≅ ∆PQR.
Given: BE and CF are two equal altitudes of a triangle ABC.
To Prove: ∆ABC is isosceles.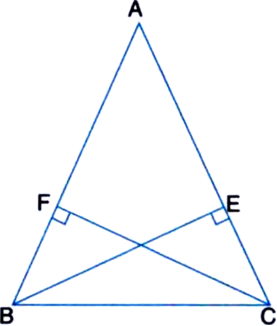
Proof: In right ∆BEC and right ∆CFB,
Side BE = Side CF | Given
Hyp. BC = Hyp. CB | Common
∴ ∆BEC ≅ ∆CFB | RHS Rule
∴ ∠BCE = ∠CBF | C.P.C.T.
∴ AB = AC
| Sides opposite to equal angles of a triangle are equal
∴ ∆ABC is isosceles.
The diagonals PR and QS of a quadrilateral PQRS intersect each other at O. Prove that
(i) PQ + QR + RS + SP > PR + QS
(ii) PQ + QR + RS + SP < 2 (PR + QS)
