811.

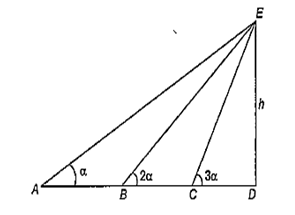
A tower subtends angles $\mathrm{\alpha }, 2\mathrm{\alpha } \mathrm{and} 3\mathrm{\alpha }$ respectively at points A, B and C, all lying on a horizontal line through the foot of the tower,then $\frac{\mathrm{AB}}{\mathrm{BC}}$ is equal to :

• $\frac{\sin \left(3\mathrm{\alpha }\right)}{\sin \left(2\mathrm{\alpha }\right)}$

• $1 + 2\cos \left(2\mathrm{\alpha }\right)$

• $2\cos \left(2\mathrm{\alpha }\right)$

• $\frac{\sin \left(2\mathrm{\alpha }\right)}{\sin \left(\mathrm{\alpha }\right)}$

The co-ordinate axes are rotated through an angle 135°. If the co-ordinates of a point P inthe new system are known to be (4, - 3), then the co-ordinates of P in the original system are :

• $\left(\frac{1}{\sqrt{2}}, \frac{7}{\sqrt{2}}\right)$

• $\left(\frac{1}{\sqrt{2}}, - \frac{7}{\sqrt{2}}\right)$

• $\left(- \frac{1}{\sqrt{2}}, - \frac{7}{\sqrt{2}}\right)$

• $\left(- \frac{1}{\sqrt{2}}, \frac{7}{\sqrt{2}}\right)$

The angle between the curves y = sin(x) and y = cos(x) is

• ${\tan }^{-1}\left(2\sqrt{2}\right)$

• ${\tan }^{-1}\left(3\sqrt{2}\right)$

• ${\tan }^{-1}\left(3\sqrt{3}\right)$

• ${\tan }^{-1}\left(5\sqrt{2}\right)$

If $\sin \left(6\mathrm{\theta }\right) = 32{\cos }^5\left(\mathrm{\theta }\right)\sin \left(\mathrm{\theta }\right) - 32{\cos }^3\left(\mathrm{\theta }\right)\sin \left(\mathrm{\theta }\right) + 3\mathrm{x}$, then x is equal to :

• $\cos \left(\mathrm{\theta }\right)$

• $\cos \left(2\mathrm{\theta }\right)$

• $\sin \left(\mathrm{\theta }\right)$

• $\sin \left(2\mathrm{\theta }\right)$

$\mathrm{The} \mathrm{period} \mathrm{of} \mathrm{the} \mathrm{function} \mathrm{f}\left(\mathrm{\theta }\right) = \sin \left(\frac{\mathrm{\theta }}{3}\right) + \cos \left(\frac{\mathrm{\theta }}{2}\right) \mathrm{is}$

• $3\mathrm{\pi }$

• $6\mathrm{\pi }$

• $9\mathrm{\pi }$

• $12\mathrm{\pi }$

$\cos \left(\mathrm{\alpha }\right)\sin \left(\mathrm{\beta } - \mathrm{\gamma }\right) + \cos \left(\mathrm{\beta }\right)\sin \left(\mathrm{\gamma } - \mathrm{\alpha }\right) + \cos \left(\mathrm{\gamma }\right)\sin \left(\mathrm{\alpha } - \mathrm{\beta }\right) \mathrm{is} \mathrm{equal} \mathrm{to}$

• 0

• $\frac{1}{2}$

• 1

• $4\cos \left(\mathrm{\alpha }\right)\cos \left(\mathrm{\beta }\right)\cos \left(\mathrm{\gamma }\right)$

$\mathrm{The} \mathrm{value} \mathrm{of} \cos \left(\frac{2\mathrm{\pi }}{15}\right)\cos \left(\frac{4\mathrm{\pi }}{15}\right)\cos \left(\frac{8\mathrm{\pi }}{15}\right)\cos \left(\frac{14\mathrm{\pi }}{15}\right) \mathrm{is} :$

• $\frac{1}{16}$

• $\frac{1}{8}$

• $\frac{1}{12}$

• $\frac{1}{4}$

If A + B + C = 270°, then
cos(2A) + cos(2B) + cos(2C) is equal to :

• 4sin(A)sin(B)sin(C)

• 4cos(A)cos(B)cos(C)

• 1 - 4sin(A)sin(B)sin(C)

• 1 - 4cos(A)cos(B)cos(C)

If ${\mathrm{x}}_{\mathrm{n}} = \cos \left(\frac{\mathrm{\pi }}{2^{\mathrm{n}}}\right) + \mathrm{isin}\left(\frac{\mathrm{\pi }}{2^{\mathrm{n}}}\right)$, then $\prod _{\mathrm{n} = 1}^{\infty }$xⁿ is equal to

• - 1

• 1

• $\frac{1}{\sqrt{2}}$

• - 3

If n $\in$ N and the period of $\frac{\cos \left(\mathrm{n\pi }\right)}{\sin \left({\displaystyle \frac{\mathrm{x}}{\mathrm{n}}}\right)}$ is 4$\mathrm{\pi }$, then n is equal to

• 4

• 3

• 2

• 1