How many sides does a regular polygon have if each of its interior angles is 165°?

12.

Question 5. (a) Is it possible to have a regular polygon with measure of each exterior angle is 22°?

 (b) Can it be an interior angle of a regular polygon? Why? 

(a) What is the minimum interior angle possible for a regular polygon? Why? (b) What is the maximum exterior angle possible for a regular polygon?

ake two identical set squares with angles 30°-60°-90° and place them adjacently to form a parallelogram as shown in Figure. Does this help you to verify the above property?

Take two identical 30°-60°-90° set-squares and form a parallelogram as before. Does the figure obtained help you to confirm the above property?

After showing m∠R = m∠N = 70°, can you find m∠I and m∠G by any other
method?

Given a parallelogram ABCD. Complete each statement along with the definition or property used.

Consider the following parallelograms. Find the values of the unknowns x, v, z.

Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

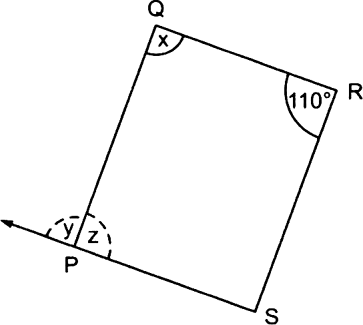
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.