Short Answer TypeQuestion 5. (a) Is it possible to have a regular polygon with measure of each exterior angle is 22°?
(b) Can it be an interior angle of a regular polygon? Why?
(a) What is the minimum interior angle possible for a regular polygon? Why? (b) What is the maximum exterior angle possible for a regular polygon?
Solution: (a) The minimum number of sides of a polygon = 3 The regular polygon of 3-sides is an equilateral.
∵ Each interior angle of an equilateral triangle = 60° Hence, the minimum possible interior angle of a polynomial = 60°
(b) ∴ The sum of an exterior angle and its corresponding interior angle is 180°.And minimum interior angle of a regular polygon = 60°
∵ The maximum exterior angle of a regular polygon = 180° - 60° = 120°
ake two identical set squares with angles 30°-60°-90° and place them adjacently to form a parallelogram as shown in Figure. Does this help you to verify the above property?
Take two identical 30°-60°-90° set-squares and form a parallelogram as before. Does the figure obtained help you to confirm the above property?
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
Long Answer TypeShort Answer TypeTwo adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
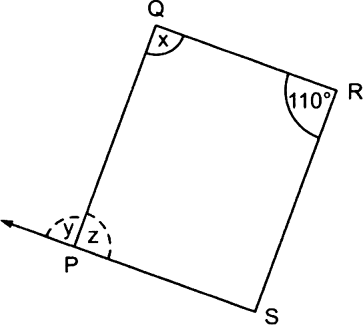
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
Switch
