Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Understanding Quadrilaterals

Short Answer Type

51.

Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that).

Figure

Side

Angle sum

180°

2 x 180°

= (4 - 2) x 180°

3 x 180°

= (5 - 2) x 180°

4 x 180°

= (6 - 2) x 180°

What can you say about the angle sum of a convex polygon with number of sides?

n

78 Views

52.

What is a regular polygon?

State the name of a regular polygon of

(i) 3 sides (ii) 4 sides (iii) 6 sides

160 Views

Long Answer Type

53.

Find the angle measure x in the following figures.

152 Views

54.

133 Views

Short Answer Type

55.

Find the measure of x in the figure.

151 Views

56.

Take a regular hexagon as shown in the figures:

What is the sum of the measures of its exterior angles x, y, z, p, q, r?

85 Views

57.
Take a regular hexagon as shown in the figures: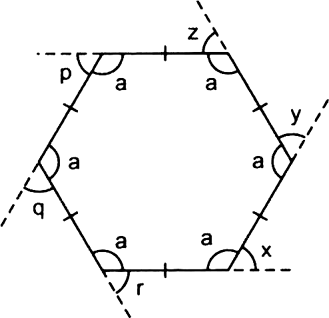

Is x = y = z = p = q = r? Why?

Since, all the sides of the polynomial are equal.

∴ It is a regular hexagon.
So, its interior angles are equal.

$space space space straight x equals space left parenthesis 180 degree minus straight a right parenthesis space space space space space space space space space space space space space straight y space equals space left parenthesis 180 degree minus straight a right parenthesis space space space straight z space equals space left parenthesis 180 degree minus straight a right parenthesis space space space space space space space space space space space space straight p space space equals space left parenthesis 180 degree minus straight a right parenthesis space space space straight q space equals space left parenthesis 180 degree minus straight a right parenthesis space space space space space space space space space space space space straight r space space space equals space left parenthesis 180 degree space minus straight a right parenthesis space space space space space$

∴ x = y = z = p= q= r