 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type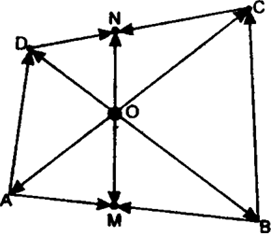
We have
![]() ...(1)
...(1)
and ![]() ...(2)
...(2)
Adding (1) and (2) we get,
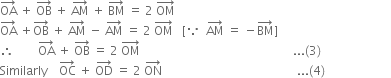
Adding (3) and (4), we get,
![]()
![]()
![]()
![]()
![]()
Also, ![]()
and ![]()
Adding, ![]()
![]()
![]()
![]()
