Long Answer Type
 are respectively 9, 7 and 6. Find the vector.
Short Answer Type
 are respectively – 1, 6 and 5. Find the vector.
Long Answer Type
Let 
           ...(1)
be the unit vector which is perpendicular to the vectors
      
                        ...(2)
      
                         ...(3)
      
                       ...(4)
Multiplying (3) by 1 and (4) by 2, we get,
x + 2y – z = 0
6x – 2y + 4z = 0
Adding, Â Â 
Multiplying (3) by 2 and (4) by 1, we get,
2x + 4y – 2z = 0
3x – y + 2z = 0
Adding, Â Â Â Â 
Putting    
      
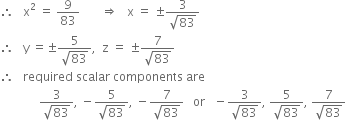
Short Answer TypeLet 
 be three vectors of magnitude 5, 3, 1 respectively. If each one is perpendicular to the sum of other two vectors, prove that 
If 
 are three mutually perpendicular vectors of equal magnitude find the angle between 
Long Answer TypeIf 
 are mutually perpendicular vectors of equal magnitude, show that they are equally inclined to the vector 
 Find a vector 
 
 Find a vector 
 which is perpendicular to both 
 and 
Switch
 show that the angle 
 between the vectors 
 is given by
 show that the angle between 
 is 
