Let ABC be the given triangle and O be the point of intersection of perpendicular bisectors OD and OE of sides BC and CA respectively.
Let F be mid-point of AB. Join O to F.
Take O as origin.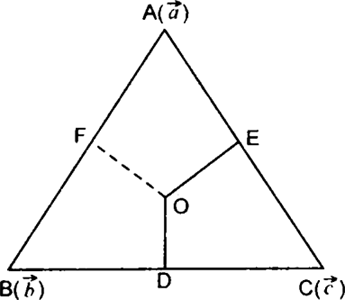

Let  be the position vectors of A, B, C respectively.
            
The position vectors of D, E, F are  respectively.
Since               

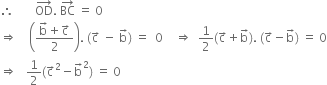
Again, 

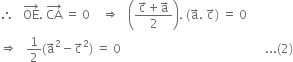
Adding (1) and (2), we get,
              

    perpendicular bisectors meet in a point.