225.
If the median of the base of a triangle is perpendicular on the base, then prove that the triangle is an isosceles.
Let ABC be a triangle in which the median AD is perpendicular to base BC.Take A as origin. Let

be position vectors of B and C so that

.
Since D is mid-point of BC
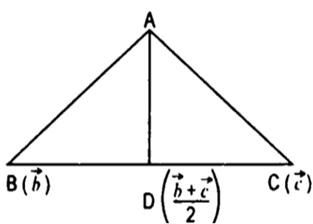

position vector of D is
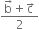
i.e.,

Also,
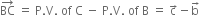
Since

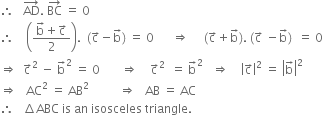
90 Views
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type
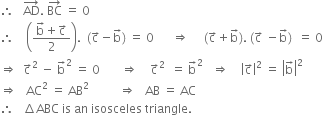
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type