Long Answer TypeProve, using vectors, that the altitudes of a triangle are concurrent.
OR
Prove that the perpendicular from the vertices to the opposite sides of a triangle are concurrent.
be the position vectors of B and D respectively so that
BC is equal and parallel to AD]
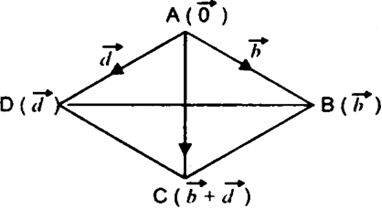
∴ position vector of mid-point of diagonal AC is same as position vector of mid-point of diagonals BD.
∴ diagonals AC and BD bisect each other.
Also, 
[
AD = AB as all sides of rhombus are equal]
diagonals AC and BD are perpendicular to each other.
Hence the result.
Short Answer TypeLong Answer TypeShort Answer Type
Switch
if 
if 
and 
then show that 
if 
