 Multiple Choice Questions
Multiple Choice QuestionsThe vectors of magnitude a, 2a, 3a meet at a point and their directions are along the diagonals of three adjacent faces of a cube. Then, the magnitude of their resultant is
5a
6a
10a
9a
A.
5a
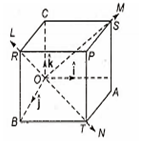
Suppose that the sides of cube are unity and unit vector along OA, OB and OC are respectively. OR, OS, OT are diagonals of cube having corresponding vector a, 2a and 3a (Magnitude) respectively.
Let A(1, - 1, 2) and B (2, 3, - 1) be two points. If a point P divides AB internally in the ratio 2 : 3, then the position vector of P is
If the scalar product of the vector with the unit vector along is equal to 2, then one of the values of m is
3
4
5
6
