Four different receptors viz, A, B, C, and D bond to the same ligand X. In order to determine which receptor has the highest binding affinity following experiment was carried out. Cells were transfected with green fluorescence protein (GFP)-tagged receptors (A, B, C, and D) individually, then incubated with red fluorescence (RFP)-tagged -'X' and subjected to FACS analysis. Following are the results

Which receptor has the highest ligand binding affinity?

• A

• B

• C

• D

During line transect sampling of two solitary species of ground mammals the following observation was made:

		Smaller species	Larger species
A	Transect length	100 km	100 km
B	No. of animals sighted	30	36
C	Mean perpendicular distance from transect line	10 m	40 m

Which of the following can be inferred from the data?

• The smaller species is ore abundant but seen less frequently.

• The smaller species are less abundant and seen less frequently.

• The larger species are more abundant but seen less frequently.

• The larger species are seen more frequently, but its abundance cannot be compared with the smaller species.

A protein contains 2 Trp and 4 Tyr residues. The molecular mass of the protein is 17000 D and that of Trp and try ae 204 and 180 D respectively. Values of E${}_{1\mathrm{cm}}^{1\%}$, the absorption coefficient of 1% (g/ v) solutions of Trp and Tyr in a 1-cm cell at 280 nm, are 269.60 and 8.33 respectively. The absorption of 1 mg/ ml protein solution in 1-cm cell at 280 nm will be:

• 0.1

• 1.0

• 0.7

• 1.7

A 16.2 m long wooden log has a uniform diameter of 2 m. To what length the log should be cut to obtain a piece of 22 m³ volume?

• 3.5 m

• 7.0 m

• 14.0 m

• 22.0 m

What is the last digit of 7⁷³?

• 7

• 9

• 3

• 1

A lucky man finds 6 pots of gold coins. He counts the coins in the first four pots to be 60, 30, 20 and 15, respectively. If there is a definite progression, what would be the numbers of coins in the next two pots?

• 10 and 5

• 4 and 2

• 15 and 15

• 12 and 10

137.

A bee leaves its hive in the morning and after flying for 30 minutes due south reaches a garden and spends 5 minutes collecting honey. Then it flies for 40 minutes due west and collects honey in another garden for 10 minutes. Then it returns to the hive taking the shortest route. How long was the bee away from its hive? (Assume that the bee flies at constant speed)

• 85 min

• 155 min

• 135 min

• Less than 1 hour

A bird perched at the top of a 12 m high tree sees a centipede moving toward the base of the tree from a distance equal to twice the height of the tree. The bird flies along a straight line to catch the centipede. If both move at the same speed, at what distance from the base of the tree will the centipede be picked up by the bird?

• 16 m

• 9 m

• 12 m

• 14 m

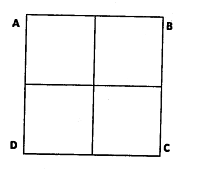
An ant goes from A to C in the figure crawling only on the lines and taking the least length of path. The number of ways in which it can do so is

• 2

• 4

• 5

• 6

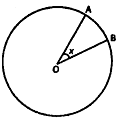
A point is chosen at random from a circular disc shown below. What is the probability that the point lies in the sector OAB?

• $\frac{2\mathrm{x}}{\mathrm{\pi }}$

• $\frac{\mathrm{x}}{\mathrm{\pi }}$

• $\frac{\mathrm{x}}{2\mathrm{\pi }}$

• $\frac{\mathrm{x}}{4\mathrm{\pi }}$