 Multiple Choice Questions
Multiple Choice QuestionsTwenty two metres are available to fence a flower bed in the form of a circular sector. If the flower bed should have the greatest possible surface area, the radius of the circle must be :
4 m
3 m
6 m
5 m
The value of x for which the polynomial 2x3 - 9x2 + 12x + 4 is a decreasing function of x, is :
- 1 < x < 1
0 < x < 2
x > 3
1 < x < 2
The length of the longest size rectangle of maximum area that can be inscribed in a semicircle of radius 1, so that 2 vertices lie on the diameter, is :
2
A.
Let the length and breadth of the rectangle be l and b.
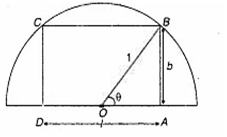
On differentiating w.r.t. , we get
Put for maxima or minima
If a particle moves such that the displacement is proportional to the square of the velocity acquired, then its acceleration is :
proportional to s2
proportional to
proportional to s
a constant
The function f(x) = tan-1(sin(x) + cos(x)), x > 0 is always an increasing function on the interval :
The radius of a cylinder is increasing at the rate of 3 m/s and its altitude is decreasing at the rate of 4 m/s. The rate of change of volume when radius is 4 m and altitude is 6 m, is :
A ladder 10 m long rests against a vertical wall with the lower end on the horizontal ground. The lower end of the ladder is pulled along the ground away from the wall at the rate of 3 emfs. The height of the upper end while it is descending at the rate of 4 emfs, is :
4
5
5
6 m
The equation of the tangent to the curve
x - y + 1 = 0
x + y + 1 = 0
2x - y + 1 = 0
x + 2y + 2 = 0
