 Multiple Choice Questions
Multiple Choice QuestionsThe maximum area of the rectangle that can be inscribed in a circle of radius r, is
r2
2r2
D.
2r2
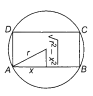
It can be easily checked that < 0 for this value of x.
A is maximum for x = and the maximum value of A is given by
The velocity of a particle at time t is given by the relation v = 6t - . The distance traveled in 3 s is, if s = 0 at t = 0
The maximum value of function x3 - 12x2 + 36x + 17 in the interval [1, 10] is
17
177
77
None of these
The abscissae of the points, where the tangent is to curve y = x3 - 3x2 - 9x + 5 is parallel to x-axis, are
x = 0 and 0
x = 1 and - 1
x = 1 and - 3
x = - 1 and 3
The equation of motion of a particle moving along a straight line is s = 2t3 - 9t2 + 12t, where the units of s and t are centimetre and second. The acceleration of the particle will be zero after
1 s
The equation of tangent to the curve y2 = ax2 + b at point (2, 3) is y = 4x - 5, then the values of a and b are
3, - 5
6, - 5
6, 15
6, - 15
