 Multiple Choice Questions
Multiple Choice QuestionsIf m and M respectively denote the minimum and maximum of f(x) = (x - 1)2 + 3 for x [- 3, 1], then the ordered pair (m, M) is equal to
(- 3, 19)
(3, 19)
(- 19, 3)
(- 19, - 3)
There is an error of cm in the measurement of the diameter of a sphere. When radius is 10cm, the percentage error in the volume of the sphere is
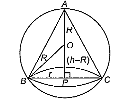
The height of the cone of maximum volume inscribed in a sphere of radius R is
C.
Let the height of the cone = h
and the radius of the cone = r
Given, radius of the sphere = R
Now, In
If the distance s travelled by a particle in time t is given by s = t2 - 2t + 5, then its acceleration is
0
1
2
3
