 Multiple Choice Questions
Multiple Choice QuestionsThe area of the region bounded by the curve , its tangent at (1, 1) and X-axis, is
sq units
sq units
Area of the region bounded by + 2 is
4 sq units
3 sq units
2 sq units
1 sq units
C.
2 sq units
In figure, B = (0, 2)
and OABC is a square.
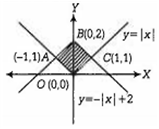
So, side of length = units
If . Then, the area of the region enclosed by the curve y = f (x) and the three lines y = x, x = 1and x = 8 is
The area of the region enclosed between parabola y2 = x and the line y = mx is . Then, the value of m is
- 2
- 1
1
2
The area of the region, bounded by the curves y = sin- 1(x) + x(1 - x) and y = sin- 1 (x) - x(1 - x) in the first quadrant, is
1
