The area of the region bounded by the curve $\mathrm{y} = {\mathrm{x}}^3$, its tangent at (1, 1) and X-axis, is

• $\frac{1}{12} \mathrm{sq} \mathrm{units}$

• $\frac{1}{6} \mathrm{sq} \mathrm{units}$

• $\frac{2}{17}$ sq units

• $\frac{2}{15}$ sq units

Area of the region bounded by $\mathrm{y} = \left|\mathrm{x}\right| \mathrm{and} \mathrm{y} = - \left|\mathrm{x}\right|$ + 2 is

• 4 sq units

• 3 sq units

• 2 sq units

• 1 sq units

The area of the region bounded by the curves y = x² and x = y² is

• 1/3

• 1/2

• 1/4

• 3

If $\mathrm{f}\left(\mathrm{x}\right) = {\mathrm{x}}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}, \mathrm{x} \ge 0$. Then, the area of the region enclosed by the curve y = f (x) and the three lines y = x, x = 1and x = 8 is

• $\frac{63}{2}$

• $\frac{93}{5}$

• $\frac{105}{7}$

• $\frac{129}{10}$

If f(x) = $\mathrm{x}\left(\frac{1}{\mathrm{x} - 1} + \frac{1}{\mathrm{x}} + \frac{1}{\mathrm{x} + 1}\right), \mathrm{x}> 1$. Then,

• $\mathrm{f}\left(\mathrm{x}\right) \le 1$

• $1 < \mathrm{f}\left(\mathrm{x}\right) \le 2$

• $2 < \mathrm{f}\left(\mathrm{x}\right) \le 3$

• $\mathrm{f}\left(\mathrm{x}\right) > 3$

36.

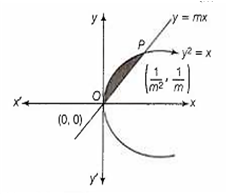
The area of the region enclosed between parabola y² = x and the line y = mx is $\frac{1}{48}$. Then, the value of m is

• - 2

• - 1

• 1

• 2

The area of the region bounded by the curves y = x , y = $\frac{1}{\mathrm{x}}$, x = 2 is

• 4 - ${\log }_{\mathrm{e}}\left(2\right)$

• $\frac{1}{4} + {\log }_{\mathrm{e}}\left(2\right)$

• $3 - {\log }_{\mathrm{e}}\left(2\right)$

• $\frac{15}{4} - {\log }_{\mathrm{e}}\left(2\right)$

The area of the region, bounded by the curves y = sin- ¹(x) + x(1 - x) and y = sin^{- 1} (x) - x(1 - x) in the first quadrant, is

• 1

• $\frac{1}{2}$

• $\frac{1}{3}$

• $\frac{1}{4}$

The area enclosed between y² = x and y = x is

• $\frac{2}{3}$ sq unit

• $\frac{1}{2}$ unit

• $\frac{1}{3}$ unit

• $\frac{1}{6}$

The area bounded by y² = 4x and x = 4y is

• $\frac{20}{3}$ sq units

• $\frac{16}{3}$ sq units

• $\frac{14}{3}$

• $\frac{10}{3}$