The area bounded by the curves y = cos(x) and y = sin(x ) between the ordinates x = 0 and x = 3π/2

• ( 4√2 - 2 ) sq units

• ( 4√2 + 2 ) sq units

• ( 4√2 - 1 ) sq units

• ( 4√2 + 1 ) sq units

The area of the region bounded by the curves x² + y² = 9 and x + y = 3 is

The area in the first quadrant between x² + y² = ${\mathrm{\pi }}^2$ and y = sin(x) is

The area bounded by y = xe^lxl and lines lxl = 1, y = 0 is,

• 4 sq units

• 6 sq units

• 1 sq unit

• 2 sq unit

For which of the following values of m, the area of the region bounded by the curve y = x - x² and the line y = mx equals 9/2

• - 4

• - 2

• 2

• 4

56.

Area lying in the first quadrant and bounded by the circle x² + y² = 4, the line x = √3y and x - axis is

• π sq units

• π/2 sq units

• π/3 sq units

• None of these

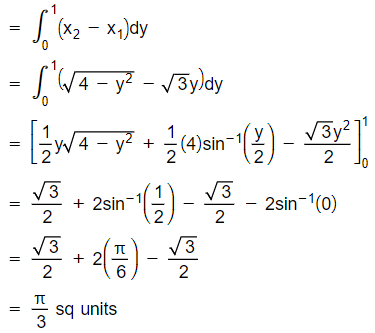
The area enclosed by y = 3x - 5, y = 0, x = 3 and x = 5 is

• 12 sq units

• 13 sq units

• $13\frac{1}{2}$ sq units

• 14 sq units

The area bounded by the curve y = | sin(x) |, x-axis and the lines | x | = π, is

• 2 sq unit

• 1 sq unit

• 4 sq unit

• None of these

The line $\mathrm{x} = \frac{\mathrm{\pi }}{4}$ divides the area of the region bounded by y = sin(x), y = cos(x) and x - axis $\left(0 \le \mathrm{x} \le \frac{\mathrm{\pi }}{2}\right)$ into two regions of areas A₁ and A₂. Then, A₁ : A₂ equals

• 4 : 1

• 3 : 1

• 2 : 1

• 1 : 1

The area of the region bounded by the straight lines x = 0 and x = 2^x and the curves y = 2 and y = 2x - x² is equal to

• $\frac{2}{\log \left(2\right)} - \frac{4}{3}$

• $\frac{3}{\log \left(2\right)} - \frac{4}{3}$

• $\frac{1}{\log \left(2\right)} - \frac{4}{3}$

• $\frac{4}{\log \left(2\right)} - \frac{3}{2}$