 Multiple Choice Questions
Multiple Choice QuestionsThe figure shows a triangle AOB and the parabola y = x2. The ratio of the area of the triangle AOB to the area of the region AOB of the parabola y = x is equal to

The area of the plane region bounded by the curve x = y2 - 2 and the· line y = - x is (in square units)
C.
Given curves x = y2 - 2 and y = x
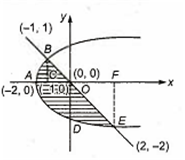
Thus, interection point are
(- 1, 1) and (2, - 2)
We are to find the area of shaded part
Area of ABC =
=
Area of BCO =
Area of ADO
Area of ODE = area of ODEF - area of OPE
[ neglecting the negative sign]
=
=
=
= sq unit
Area bounded by the curve y = log (x - 2), x-axis and x = 4 is equal to
2log(2) + 1
log(2) - 1
log(2) + 1
2log(2) - 1
