 Multiple Choice Questions
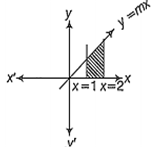
Multiple Choice QuestionsThe area of the region bounded by the lines y = mx, x = 1, x = 2 and x-axis is 6 sq units, then 'm' is
3
1
2
4
D.
4
Given, equation of line is y = mx and bounded by x = 1, x = 2 and x-axis
Area of the region bounded by the curve y = cos(x), x = 0 and x = is
4 sq unit
3 sq units
1 sq units
2 sq units
The area bounded by the curves y2 - x = 0 and y - x2 = 0, is
7/3 sq unit
1/3 sq unit
5/3 sq unit
1 sq unit
Area between the curve y = cos(x) and X - axis, when , is
0 sq units
2 sq units
3 sq units
4 sq units
The area bounded by the X - axis, the curve y = f(x) and the lines x = 1, x = b and is equal to for all b > 1, then f(x) is
