 Multiple Choice Questions
Multiple Choice QuestionsLet A(- 1, 0) and B(2, 0) be two points. A point M moves in the plane in such a way that . Then, the point M moves along
a straight line
a parabola
an ellipse
a hyperbola
The area of the figure bounded by the parabolas x = - 2y 2 and x = 1- 3y2 is
sq. units
sq. units
sq. units
sq. units
A.
sq. units
We have,
x = - 2y2
y2 = - ...(i)
and x = 1 - 3y2
y2 = - ...(ii)
From equation (i) and (ii), we get
= 1
Point of intersection of two curves is (- 2, ± 1)
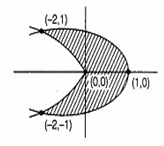
Required area =
=
=
= sq. uniys
Tangents are drawn to the ellipse at the ends of both latusrectum. The area of the quadrilateral, so formed is
27 sq. units
sq. units
sq. units
45 sq. units
If the tangent to y2 = 4ax at the point (at2, 2at) where > 1 is a normal to x2 - y2 = a2 at the point (), then
The equation of a line parallel to the line 3x + 4y= 0 and touching the circle x2 + y2 = 9 in the first quadrant, is
3x +4y = 15
3x +4y = 45
3x +4y = 9
3x +4y = 27
A line passing through the point of intersection of x + y = 4 and x - y = 2 makes an angle with the x-axis. It intersects the parabola y2 = 4(x-3) at points respectively. Then,
The equation of auxiliary circle of the ellipse 16x2 + 25y2 + 32x - 100y = 284 is
x2 + y2 + 2x - 4y - 20 = 0
x2 + y2 + 2x - 4y = 0
(x + 1)2 + (y - 2)2 = 400
(x + 1)2 + (y - 2)2 = 225
If PQ is a double ordinate of the hyperbola is equilateral. O being the centre. Then, the eccentricity e satisfies
e =
e =
