 Multiple Choice Questions
Multiple Choice QuestionsThe locus of the passes through (a, 0), (- a, 0) is the centre of a circle which two variable points
x = 1
x + y = a
x + y = 2a
x = 0
The intercept on the line y = x by the circle x2 = y2 - 2x = 0 is AB. Equation of the circle with AB as the diameter is
x2 + y2 = 1
x(x - 1) + y(y - 1) = 0
x2 + y2 = 2
(x - 1)(x - 2) + (y - 1)(y - 2) = 0
If the coordinates of one end of a diameter of the circle x2 + y2 + 4x-8y + 5 = 0 are (2, 1), the coordinates of the other end are
(- 6, - 7)
(6 , 7)
(- 6, 7)
(7, - 6)
The locus of the middle points of all chords of the parabola y2 = 4ax passing through the vertex is
a straight line
an ellipse
a parabola
a circle
C.
a parabola
Let OB be a chord and let B(h, k).
Then, coordinate of M be .
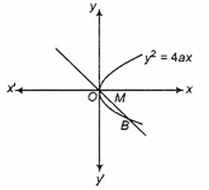
But (h, k) lies on the parabola.
 Short Answer Type
Short Answer TypeProve that the centre of the smallest circle passing through origin and whose centre lies on y = x + 1 is
 Multiple Choice Questions
Multiple Choice QuestionsIf t1 and t2 be the parameters of the end points of a focal chord for the parabola y2 = 4ax, then which one is true?
t1t2 = 1
t1t2 = - 1
t1 + t2 = - 1
S and T are the foci of an ellipse and B is end point of the minor axis. If STB is an equilateral triangle, the eccentricity of the ellipse is
For different values of a, the locus of the point of intersection of the two straight lines and
a hyperbola with eccentricity 2
an ellipse with eccentricity
a hyperbola with eccentricity
an ellipse with eccentricity
The circles x2 + y2 - 10x + 16 = 0 and x2 + y2 = a2 intersect at two distinct points, if
a < 2
2 < a < 8
a > 8
a = 2
For the two circles x2 + y2 = 16 and x2 + y2 - 2y = 0 there is/are
one pair of common tangents
only one common tangent
three common tangents
no common tangent
