 Multiple Choice Questions
Multiple Choice QuestionsThe equation of the tangent to the conic x2 - y2 - 8x + 2y + 11 = 0 at (2, 1) is
x + 2 = 0
2x + 1 = 0
x + y + 1 = 0
x - 2 = 0
The total number of tangents through the point ( 3, 5) that can be drawn to the ellipses 3x2 + 5y2 = 32 and 25x + 9y2 = 450 is
0
2
3
4
C.
3
Let S1 = 3x2 + 5y2 - 32
and S2 = 25x2 + 9y2 - 450
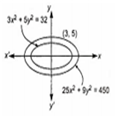
At point (3, 5)
S1 = 3(3)2 + 5(5)2 - 32 = 120 > 0
and S2 = 25(3)2 + 9(5)2 - 450
= 225 + 225 - 450 = 0
Thus, Point (3, 5) lies outside the first ellipse and for second ellipse lies on the ellipse.
Hence, two tangents for first ellipse and one tangent for second ellipse can be drawn.
The equation of chord of the circle x2 + y2 - 4x = 0, whose mid-point is (1, 0) is
y = 2
y = 1
x = 2
x = 1
The coordinates of the focus of the parabola described parametrically by x = 5t2 + 2, y = 10t + 4 are
(7, 4)
(3, 4)
(3, - 4)
(- 7, 4)
The angle between the lines joining the foci of an ellipse to one particular extremity of the minor axis is 90°. The eccentricity of the ellipse is
1/8
1/√3
√(2/3)
√(1/2)
If the rate of increase of the radius of a circle is 5 cm/ s, then the rate of increase of its area, when the radius is 20 cm, will be
10
20
200
400
The equation of the circle which passes through the points of intersection of the circles x2 + y2 - 6x = 0 and x2 + y2 - 6y = 0 and has its centre at , is
x2 + y2 + 3x + 3y + 9 = 0
x2 + y2 + 3x + 3y = 0
x2 + y2 - 3x - 3y = 0
x2 + y2 - 3x - 3y + 9 = 0
If 2y = x and 3y + 4x = 0 are the equations of a pair of conjugate diameters of an ellipse, then the eccentricity of the ellipse is
If t is a parameter, then x = , y = represents
an ellipse
a circle
a pair of straight lines
a hyperbola
