 Short Answer Type
Short Answer TypeProve that for all values of m, except zero the straight line
y = mx + touches the parabola y2 = 4ax.
 Multiple Choice Questions
Multiple Choice QuestionsIf the lines 3x - 4y - 7 = 0 and 2x - 3y - 5 = 0 are two diameters of a circle of area 49 sq unit, then equation of the circle is
x2 + y2 + 2x - 2y - 62 = 0
x2 + y2 - 2x + 2y - 62 = 0
x2 + y2 - 2x + 2y - 47 = 0
x2 + y2 + 2x - 2y - 47 = 0
The locus of middle point of chords of hyperbola 3x2 - 2y2 + 4x - 6y = 0 parallel to y = 2x is
3x - 4y = 4
3x - 4x + 4 = 0
4x - 3y = 3
3x - 4y = 2
The equation of the common tangent touching the circle (x - 3)2 + y2 = 9 and parabola y = 4x above the x-axis is
√3y = 3x + 1
√3y = -( x + 3 )
√3y = x + 3
√3y = -( 3x + 1 )
C.
√3y = x + 3
Any tangent to y2 = 4x is y = ![]() . It touches the circle, if 3 =
. It touches the circle, if 3 = 
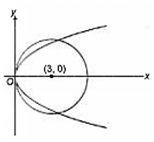
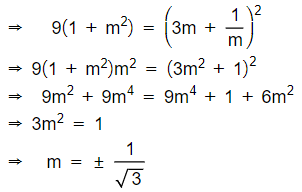
For the common tangent to the above x-axis we take
m = 1/√3
∴ Equation of common tangent is,

The equation of the tangents to the ellipse 4x2 + 3y2 = 5 which are parallel to the line y = 3x + 7 are
None of these
The radius of the circle passing through the foci of the ellipse and having its centre (0, 3) is
4
3
7/2
The equation of the circle on the common chord of the circles (x - a)2 + y2 = a2 and x2 + (y + b)2 = b2 as diameter is
x2 + y2 = 2ab(bx + ay)
x2 + y2 = bx + ay
(a2 + b2)(x2 + y2) = 2ab(bx - ay)
(a2 + b2)(x2 + y2) = 2(bx + ay)
The line x - 1 = 0 is the directrix of the parabola y2 - kx + 8 = 0. Then, one of the value of k is
8
4
