The radius of the sphere x² + y² + z² = 12x + 4y + 3z is

• 13/2

• 13

• 26

• 52

The centre and radius of the sphere x² + y² + z² + 3x - 4z + 1 = 0 are

• $\left(- \frac{3}{2}, 0, - 2\right); \frac{\sqrt{21}}{2}$

• $\left(\frac{3}{2}, 0, 2\right); \sqrt{21}$

• $\left(- \frac{3}{2}, 0, 2\right); \frac{\sqrt{21}}{2}$

• $\left(- \frac{3}{2}, 0, 2\right); \frac{21}{2}$

Let A and B are two fixed points in a plane, then locus of another point Con the same plane such that CA + CB = constant, (> AB) is

• circle

• ellipse

• parabola

• hyperbola

The directrix of the parabola y² + 4x + 3 = 0 is

• $\mathrm{x} - \frac{4}{3} = 0$

• $\mathrm{x} + \frac{1}{4} = 0$

• $\mathrm{x} - \frac{3}{4} = 0$

• $\mathrm{x} - \frac{1}{4} = 0$

The length of the parabola y² = 12x cut off by the latusrectum is

• $6\left[\sqrt{2} + \log \left(1 + \sqrt{2}\right)\right]$

• $3\left[\sqrt{2} + \log \left(1 + \sqrt{2}\right)\right]$

• $6\left[\sqrt{2} - \log \left(1 + \sqrt{2}\right)\right]$

• $3\left[\sqrt{2} - \log \left(1 + \sqrt{2}\right)\right]$

Area enclosed by the curve $\mathrm{\pi }\left[4{\left(\mathrm{x} - \sqrt{2}\right)}^2 + {\mathrm{y}}^2\right] = 8$ is

• $\mathrm{\pi }$ sq unit

• 2 sq unit

• 3$\mathrm{\pi }$ sq unit

• 4 sq unit

The equation of a directrix of the ellipse $\frac{{\mathrm{x}}^2}{16} + \frac{{\mathrm{y}}^2}{25} = 1$ is :

• 3y = 5

• y = 5

• 3y = 25

• y = 3

If the normal at (ap, 2ap) on the parabola y² = 4ax, meets the parabola again at (aq² , 2aq), then

• p² + pq + 2 = 0

• p² - pq + 2 = 0

• q² + pq + 2 = 0

• p² + pq + 1

The curve described parametrically by x = t² + 2t - 1, y = 3t + 5 represents :

• an ellipse

• a hyperbola

• a parabola

• a circle

210.

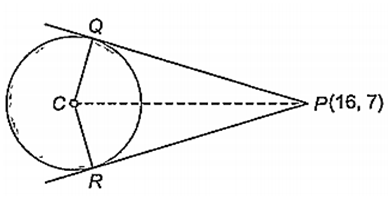
From the point P (16, 7), tangents PQ and PR are drawn to the circle x² + y² - 2x - 4y - 20 = 0. If C is the centre of the circle, then area of the quadrilateral PQCR is

• 15 sq unit

• 50 sq unit

• 75 sq unit

• 150 sq unit