If the line x + 2by + 7 = 0 is a diameter of the circle x² + y² - 6x + zy = 0, then b is equal to

• - 5

• - 3

• 2

• 5

If the line y = 2x+ c is tangent to the parabola y² = 4x, then c is equal to

• $- \frac{1}{2}$

• $\frac{1}{2}$

• $\frac{1}{3}$

• $\frac{1}{4}$

The length of the latus rectum of the ellipse 9x² + 4y² = 1 is

• $\frac{3}{2}$

• $\frac{4}{9}$

• $\frac{8}{3}$

• $\frac{8}{9}$

264.

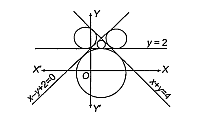
The number of circles that touch all the straight lines x + y = 4,x - y = - 2 and y = 2 is

• 1

• 2

• 3

• 4

The equation of the normal to the circle x² + y² + 6x + 4y - 3 = 0 at (1, - 2) is

• y + 1 = 0

• y + 2 = 0

• y + 3 = 0

• y - 2 = 0

The limiting points of the co-axial system containing the two circles x² + y² + 2x - 2y + 2 = 0 and 25(x² + y) - 10x - 80y + 65 = 0 are

• (1, - 1), (- 3, - 40)

• $\left(1, - 1\right), \left(- \frac{1}{5}, \frac{8}{5}\right)$

• $\left(- 1, 1\right), \left(\frac{1}{5}, \frac{8}{5}\right)$

• $\left(- \frac{1}{5}, - \frac{8}{5}\right)$

The radical axis of circles x² + y² + 5x + 4y - 5 = 0 and x² + y² - 3x + 5y - 6 = 0 is

• 8y - x + 1 = 0

• 8x - y+ 1 = 0

• 8x - 8y + 1 = 0

• y - 8x + 1 = 0

The length of latusrectum of parabola y² + 8x - 2y + 17 = 0 is

• 2

• 4

• 8

• 16

If the normal to the parabola y² = 4x at P(1, 2) meets the parabola again in Q, then coordinates of Q are

• (- 6, 9)

• (9, - 6)

• (- 9, - 6)

• (- 6, - 9)

The eccentricity of ellipse $\frac{{\mathrm{x}}^2}{16} + \frac{{\mathrm{y}}^2}{9} = 1$ is

• $\frac{7}{16}$

• $\frac{5}{4}$

• $\frac{\sqrt{7}}{4}$

• $\frac{\sqrt{7}}{2}$