 Multiple Choice Questions
Multiple Choice QuestionsIf is the angle between the tangents from(- 1, 0) to the circle x2 + y2 - 5x + 4y - 2 = 0, then is equal to
If 2x + 3y + 12 = 0 and x - y + 4 = 0 are conjugate with respect to the parabola y = 8x, then is equal to
2
- 2
3
- 3
For an ellipse with eccentricity the centre is at the origin. If one directrix is x = 4, then the equation of the ellipse is
The area (in square unit) of the circle which touches the lines 4x + 3y = 15 and 4x + 3y = 5 is
4
The equations of the circle which pass through the origin and makes intercepts of length 4 and 8 on the x and y-axes respectively are
The locus of centre of a circle which passes through the origin and cuts off a length of 4 unit from the line x = 3 is
y2 + 6x = 0
y2 + 6x = 13
y2 + 6x = 10
x2 + 6y = 13
B.
y2 + 6x = 13
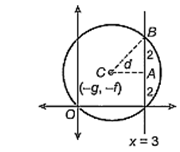
Hence, required locus is y2 + 6x = 13
The diameters of a circle are along 2x +y - 7 and x + 3y - 11 = 0. Then, the equation of this circle, which also passes through (5, 7) is
