• 3x² + 3y² - 8x - 13y = 0

• 3x² + 3y² - 8x + 29y = 0

• 3x² + 3y² + 8x + 29y = 0

• 3x² + 3y² - 8x - 29y = 0

332.

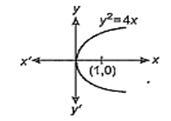
The number of normals drawn to the parabola y² = 4x from the point (1, 0) is

• 0

• 1

• 2

• 3

If the distance between foci of an ellipse is 6 and the length of the minor axis is 8, then the eccentricity is

• $\frac{1}{\sqrt{5}}$

• $\frac{1}{2}$

• $\frac{3}{5}$

• $\frac{4}{5}$

If the circle x² + y² = a² intersects the hyperbola xy = c² in four points (x_i, y_i), for i = 1, 2, 3 and 4, then y₁ + y₂ + y₃ + y₄ equals

• 0

• c

• a

• c⁴

The mid point of the chord 4x - 3y = 5 of the hyperbola 2x² - 3y² = 12 is

• $\left(0, - \frac{5}{3}\right)$

• (2, 1)

• $\left(\frac{5}{4}, 0\right)$

• $\left(\frac{11}{4}, 2\right)$

$$\begin{gathered} \mathrm{The} \mathrm{eccentricity} \mathrm{of} \mathrm{conic} \\ \frac{5}{\mathrm{r}} = 2 +\hspace{0.17em}3\cos \left(\mathrm{\theta }\right) + 4\sin \left(\mathrm{\theta }\right) \mathrm{is} \end{gathered}$$

• $\frac{1}{2}$

• 1

• $\frac{3}{2}$

• $\frac{5}{2}$

$\mathrm{The} \mathrm{radius} \mathrm{of} \mathrm{the} \mathrm{sphere} {\mathrm{x}}^2 + {\mathrm{y}}^2 + {\mathrm{z}}^2 = 12\mathrm{x} + 4\mathrm{y} +\hspace{0.17em}3\mathrm{z} \mathrm{is}$

• $\frac{13}{2}$

• 13

• 26

• 52

$$\begin{gathered} \mathrm{The} \mathrm{equation} \mathrm{of} \mathrm{the} \mathrm{radical} \mathrm{axis} \mathrm{of} \mathrm{the} \mathrm{pair} \mathrm{of} \mathrm{circles} \\ 7{\mathrm{x}}^2 + 7{\mathrm{y}}^2 - 7\mathrm{x} + 14\mathrm{y} + 18 = 0 \mathrm{and} 4{\mathrm{x}}^2 + 4{\mathrm{y}}^2 - 7\mathrm{x} + 8\mathrm{y} + 20 = 0 \mathrm{is} \end{gathered}$$

• x - 2y - 5 = 0

• 2x - y + 5 = 0

• 21x - 68 = 0

• 23x - 68 = 0

$$\begin{gathered} {\mathrm{x}}^2 + {\mathrm{y}}^2 - 8\mathrm{x} + 40 = 0 \\ 5{\mathrm{x}}^2 + 5{\mathrm{y}}^2 -25\mathrm{x} + 80 = 0 \\ {\mathrm{x}}^2 + {\mathrm{y}}^2 - 8\mathrm{x} + 16\mathrm{y} + 160 = 0 \\ \mathrm{From} \mathrm{the} \mathrm{point} \mathrm{P} \mathrm{are} \mathrm{equal}, \mathrm{then} \mathrm{P} = ? \end{gathered}$$

• $\left(8, \frac{15}{2}\right)$

• $\left(- 8, \frac{15}{2}\right)$

• $\left(8, \frac{- 15}{2}\right)$

• $\left(- 8, \frac{- 15}{2}\right)$

The equation of the circle concentric with the circle x² + y² - 6x + 12y + 15 = 0 and of double its area is

• x² + y² - 6x +12y - 15 = 0

• x² + y² - 6x +12y - 30 = 0

• x² + y² - 6x +12y - 25 = 0

• x² + y² - 6x +12y - 20 = 0