Let M be the foot of the perpendicular from a point P on the parabola y = 8(x - 3) onto its directrix and let S be the focus ofthe parabola. If  $∆$SPM is an equilateral triangle, then P is equal to

• $(4\sqrt{3}, 8)$

• $(8, 4\sqrt{3})$

• $(9, 4\sqrt{3})$

• $(4\sqrt{3}, 9)$

Consider the circle x² + y - 4x - 2y + c = 0 whose centre is A(2, 1). If the point P(10, 7) is such that the line segment PA meets the circle in Q with PQ = 5, then c is equal to

• - 15

• 20

• 30

• - 20

The foci of the ellipse $\frac{{\mathrm{x}}^2}{16} + \frac{{\mathrm{y}}^2}{{\mathrm{b}}^2} = 1 \mathrm{and} \mathrm{the} \mathrm{hyperbola} \frac{{\mathrm{x}}^2}{144} - \frac{{\mathrm{y}}^2}{81} = \frac{1}{25}$ coincide. Then, the value of b² is 

• 5

• 7

• 9

• 1

The tangents to the parabola y = 4ax from an external point P make angles ${\mathrm{\theta }}_1 \mathrm{and} {\mathrm{\theta }}_2$, with the axis of the parabola. Such that $\tan \left({\mathrm{\theta }}_1\right) + \tan \left({\mathrm{\theta }}_2\right) = \mathrm{b}$ where b is constant. Then P lies on

• y = x + b

• y + x = b

• $\mathrm{y} = \frac{\mathrm{x}}{\mathrm{b}}$

• y = bx

445.

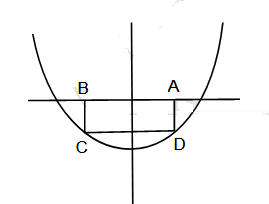
The area (in sq. units) of the largest rectangle ABCD whose vertices A and B lie on the x-axis and vertices C and D lie on the parabola, y = x² – 1 below the x-axis, is

• $\frac{1}{3\sqrt{3}}$

• $\frac{4}{3}$

• $\frac{4}{3\sqrt{3}}$

• $\frac{2}{3\sqrt{3}}$