$\underset{\mathrm{x}\to 0}{\lim }\frac{{\log }_{\mathrm{e}}\left(1 +\hspace{0.17em}\mathrm{x}\right)}{3^{\mathrm{x}} - 1}$ is equal to

• ${\log }_{\mathrm{e}}\left(3\right)$

• 0

• ${\log }_3\left(\mathrm{e}\right)$

• 1

If f(x) = $$\begin{gathered} \left\{\mathrm{x}, \mathrm{if} \mathrm{x} \mathrm{is} \mathrm{irrational} \\ 0, \mathrm{if} \mathrm{x} \mathrm{is} \mathrm{rational}\right\} \end{gathered}$$, then f is

• continuous everywhere

• discontinuous everywhere

• continuous only at x = 0

• continuous at all rational numbers

If $\mathrm{x} + \mathrm{y} = {\tan }^{-1}\left(\mathrm{y}\right) \mathrm{and} \frac{{\mathrm{d}}^2\mathrm{y}}{{\mathrm{dx}}^2} = \mathrm{f}\left(\mathrm{y}\right)\frac{\mathrm{dy}}{\mathrm{dx}}$, then f(y) is equal to

• $\frac{- 2}{{\mathrm{y}}^3}$

• $\frac{2}{{\mathrm{y}}^3}$

• $\frac{1}{\mathrm{y}}$

• $\frac{- 1}{\mathrm{y}}$

If f(x) = $$\begin{gathered} \left\{2\mathrm{a} - \mathrm{x} \mathrm{when} - \mathrm{a} < \mathrm{x} <\hspace{0.17em}\mathrm{a} \\ 3\mathrm{x} - 2\mathrm{a} \mathrm{when} \mathrm{a} \le \mathrm{x}\right\} \end{gathered}$$. Then, which of the following is true ?

• f(x) is not differentiable at x = a

• f(x) is discontinuous at x = a

• f(x) is continuous for all x < a

• f(x) is differentiable for all x $\ge$ a

If f(x) = ${\cos }^{-1}\left[\frac{1}{\sqrt{13}}\left(2\cos \left(\mathrm{x}\right) - 3\sin \left(\mathrm{x}\right)\right)\right]$. Then f'(0.5) is equal to

• 0.5

• 1

• 0

• - 1

If f(x) is a function such that f"(a) + f'(a) = 0 and g(x) =[f(x)]² + [f'(x)]² and g(3) = 8, then g(8) is equal to

• 0

• 3

• 5

• 8

If f(a) = f'(x) + f"(x) + f'"(x) + ... and f(0) = 1, then f(x) is equal to

• e^x/2

• e^x

• e^2x

• e^4x

If f(x) = x³ and g(x) = x³ - 4x in - 2 $\le \mathrm{x} \le$, then consider the statements

(i) f(x) and g(x) satisfy mean value theorem.

(ii) f(x) and g(x) both satisfy Rolle's theorem.

(iii)  Only g(x) satisfies Rolle's theorem.

Of these statements.

• (i) and (ii) are correct

• only (i) is correct

• None is correct

• (i) and (iii) are correct

If the function f(x) defined by $\mathrm{f}\left(\mathrm{x}\right) = \frac{{\mathrm{x}}^{100}}{100} + \frac{{\mathrm{x}}^{99}}{99} + ... + \frac{{\mathrm{x}}^2}{2} +\hspace{0.17em}\mathrm{x}\hspace{0.17em}+\hspace{0.17em}1$, then f'(0) is equal to

• 100f'(0)

• 100

• 1

• - 1

The function represented by the following graph is

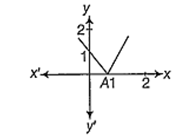
• continuous but not differentiable at x = 1

• differentiable but not continuous at x = 1

• continuous and differentiable at x = 1

• neither continuous nor differentiable at x = 1