$\mathrm{If} \mathrm{z} = \frac{\mathrm{y}}{\mathrm{x}}\left[\sin \left(\frac{\mathrm{x}}{\mathrm{y}}\right) + \cos \left(1 + \frac{\mathrm{y}}{\mathrm{x}} \right) \right], \mathrm{then} \mathrm{x}\frac{\partial \mathrm{z}}{\partial \mathrm{x}} \mathrm{is} \mathrm{equal} \mathrm{to}$

• $y\frac{\partial z}{\partial y}$

• $- \mathrm{y}\frac{\partial \mathrm{x}}{\partial \mathrm{y}}$

• $2\mathrm{y}\frac{\partial \mathrm{z}}{\partial \mathrm{y}}$

• $2\mathrm{y}\frac{\partial \mathrm{z}}{\partial \mathrm{x}}$

• 18/e⁴

• 27/e²

• 9/e²

• 9/e²

The area (in sq. units) of the region is

If a curve y=f(x) passes through the point (1, −1) and satisfies the differential equation, y(1+xy) dx=x dy, then f(-1/2) is equal to

• -2/5

• -4/5

• 2/5

• 2/5

5.

If f and ga re differentiable  functions in (0,1) satisfying f(0) =2= g(1), g(0) = 0 and f(1) = 6, then for some c ε] 0,1[

• 2f'(c) = g'(c)

• 2f'(c) = 3g'(c)

• f'(c) = g'(c)

• f'(c) = g'(c)

The population p(t) at time t of a certain mouse species satisfies the differential equation 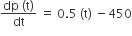. if p (0) = 850, then the  time at which the population becomes zero is

• 2 log 18

• log 9

• 
• 

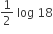
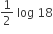
Consider the function f(x) = |x – 2| + |x – 5|, x ∈ R.
Statement 1: f′(4) = 0
Statement 2: f is continuous in [2, 5], differentiable in (2, 5) and f(2) = f(5).

• Statement 1 is false, statement 2 is true

• Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1

• Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1

• Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1

The shortest distance between line y - x = 1 and curve x = y² is

• √3/4

• 3√2 /8

• 8/3√2

• 8/3√2

• does not exist

• equal 

• equal 

• equal