A particle starts moving from rest from a fixed point in a fixed direction. The distance s from the fixed point at a time t is given by s = t² + at - b + 17, where a and b are real numbers. If the particle comes to rest after 5 s at a distance of s = 25 units from the fixed point, then values of a and b are, respectively

• 10, - 33

• - 10, - 33

• - 8, 33

• - 10, 33

If a, band c are in AP, then the straight line ax + 2by + c = 0 will always pass through a fixed point whose coordinates are

• (1, - 1)

• (- 1, 1)

• (1, - 2)

• (- 2, 1)

The number of diagonals in a regular polygon of 100 sides is

• 4950

• 4850

• 4750

• 4650

14.

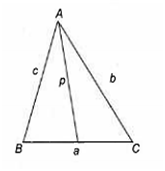
Let p, q and r be the altitudes of a triangle with area S and perimeter 2 t. Then, the value of $\frac{1}{\mathrm{p}} + \frac{1}{\mathrm{q}} + \frac{1}{\mathrm{r}}$ is

• $\frac{\mathrm{S}}{\mathrm{t}}$

• $\frac{\mathrm{t}}{\mathrm{S}}$

• $\frac{\mathrm{S}}{2\mathrm{t}}$

• $\frac{2\mathrm{S}}{\mathrm{t}}$

Let P and Q be the points on the parabola y² = 4x so that the line segment PQ subtends right angle at the vertex. If PQ intersects the axis of the parabola at R, then the distance of the vertex from R is

• 1

• 2

• 4

• 6

If the three points A(1, 6), B(3,- 4) and C(x, y) are collinear, then the equation satisfying by x and y is

• 5x + y - 11 = 0

• 5x + 13y + 5 = 0

• 5x - 13y + 5 = 0

• 13x - 5y + 5 = 0

The number of diagonals in a polygon is 20. The number of sides of the polygon is

• 5

• 6

• 8

• 10

In a right-angled triangle, the sides are a, b and c with c as hypotenuse and c - b $\ne$ 1, c + b $\ne$ 1. Then the value of (log_{c + b}(a) + log_{c - b}(a))/ (2log_{c + b}(a) x log_{c - b}(a)) will be

• 2

• - 1

• $\frac{1}{2}$

• 1

If the three points (3q, 0), (0, 3p) and (1, 1) are collinear, then which one is true?

• $\frac{1}{\mathrm{p}} +\hspace{0.17em}\frac{1}{\mathrm{q}} = 1$

• $\frac{1}{\mathrm{p}} +\hspace{0.17em}\frac{1}{\mathrm{q}} = 2$

• $\frac{1}{\mathrm{p}} +\hspace{0.17em}\frac{1}{\mathrm{q}} = 3$

• $\frac{1}{\mathrm{p}} +\hspace{0.17em}\frac{3}{\mathrm{q}} = 1$

The equation $\mathrm{y} = \pm \sqrt{3}\mathrm{x}$, y = 1 are the sides

• an equilateral triangle

• a right angled triangle

• a isosceles triangle

• an obtuse angled triangle