 Multiple Choice Questions
Multiple Choice QuestionsThe objective function of LPP defined over the convex set attains it optimum value at
atleast two of the corner points
all the corner points
atleast one of the corner points
None of the corner points
If an LPP admits optimal solution at two consecutive vertices of a feasible region, then
the LPP under consideration is not solvable
the LPP under consideration must be reconstructed
the required optimal solution is at the mid-point of the line joining two points
the optimal solution occurs at every point on the line joining these two points
By graphical method, the solution of linear programming problem maxirmze z = 3x1 + 5x2 subject to 3x1 + 2x2
x1 = 2, x2 = 0, z = 6
x1 = 2, x2 = 6, z = 36
x1 = 4, x2 = 3, z = 36
x1 = 4, x2 = 6, z = 42
If x and y are independent vanables, then the angle between lines of regression is
45°
0°
30°
90°
In a linear programming problem z = 2x + y when 5x + 10y 50, x + y 1, y 4 and x, y 0 minimum value of z is
0
1
2
1/2
B.
1
z = 2x + y
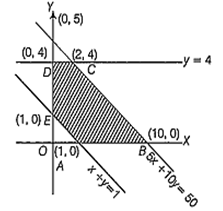
At A (1, 0), z = 2 + 0 = 2
At B (10, 0), z = 20 + 0 = 20
At C (2, 4), z = 4 + 4 = 8
At D (0, 4), z = 0 + 4 = 4
and at E (0, 1), z = 0 + 1 = 1
Thus, minimum value of z is 1.
The maximum value of z = 4x + 2y subject to the constraints 2x + 3y 18, x + y 10, x, y 0
36
40
20
None of these
The maximum value of = 3x + 4y, subject to the conditions x + y 40, x + 2y 60, x, y 0, is
130
140
40
120
If x + y 2; x 20, y 20, then the point, at which the maximumvalue of 3x + 2y is attained, will be
(0, 0)
(2, 0)
(0, 2)
