Multiple Choice QuestionsIf: R →R is a function defined by 
where [x] denotes the greatest integer function, then f is
continuous for every real x
discontinous only at x = 0
discontinuous only at non-zero integral values of x
discontinuous only at non-zero integral values of x
The value of p and q for which the function f(x) =
p = 1/2. q = -3/2
p = 5/2, q = 1/2
p = - 3/2, q = 1/2
p = - 3/2, q = 1/2
let f : (-1, 1) → R be a differentiable function
with f(0) = -1 and f'(0) = 1.
Let g(x) = [f(2f(x) + 2)]2. Then g'(0) =
4
-4
0
0
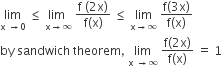
For real x, let f(x) = x3+ 5x + 1, then
f is one–one but not onto R
f is onto R but not one–one
f is one–one and onto R
f is one–one and onto R
Let f(x) = (x + 1)2– 1, x ≥ – 1
Statement – 1: The set {x : f(x) = f–1(x)} = {0, –1}.
Statement – 2: f is a bijection.
Statement–1 is true, Statement–2 is true,Statement–2 is a correct explanation for statement–1
Statement–1 is true, Statement–2 is true; Statement–2 is not a correct explanation for statement–1.
Statement–1 is true, statement–2 is false.
Statement–1 is true, statement–2 is false.
Let f(x) = x|x| and g(x) = sinx
Statement 1 : gof is differentiable at x = 0 and its derivative is continuous atthat point
Statement 2: gof is twice differentiable at x = 0
Statement–1 is true, Statement–2 is true, Statement–2 is a correct explanation for statement–1
Statement–1 is true, Statement–2 is true;Statement–2 is not a correct explanation for statement–1.
Statement–1 is true, statement–2 is false.
Statement–1 is true, statement–2 is false.
Switch
then g(x) is equals to 
[cot x]dx, where [.] denotes the greatest integer function, is equal to
