 Multiple Choice Questions
Multiple Choice QuestionsIf the distance between (2, 3) and (- 5, 2) is equal to the distance between (x, 2) and (1, 3), then the values of x are
- 6, 8
6, 8
- 8, 6
- 7, 7
The vertices of a triangle are A(3, 7), B (3, 4) and C (5, 4). The equation of the bisector of the angle ABC is
y = x + 1
y = x - 1
y = 3x - 5
y = x
If the angle between a and c is 25°, the angle between b and c is 65° and a + b = c, then the angle between a and b is
40°
115°
25°
90°
D.
90°
Let the angle between a and c is '', then = 25° and the angle between b and c is 'a', then = 65°
a + b = c ...(i)
So, by parallelogram's property
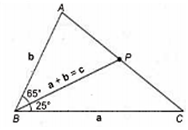
Resultant of a and b = a + b = c [from Eq. (i)]
So, angle between a and b = 25° + 65°
= 90°
The projection of the vector 2i + aj - k on the vector i - 2j + k is . Then, the value of a is equal to
1
2
- 2
3
A unit vector in the XOY-plane that makes an angle 30° with the vector i + j and makes an angle 60° with i - j is
The angle between the line r = (i + 2j + 3k) + (2i + 3j + 4k) and the plane r - (i + j - 2k) = 0 is
0°
60°
30°
90°
The lines r = i + j - k + (3i - j) and r = 4j - k + µ (2i + 3k) intersect at the point
(0, 0, 0)
(0, 0, 1)
(0, - 4, - 1)
(4, 0, - 1)
An equation of the plane through the points (1, 0, 0) and (0, 2, 0) and at a distance units from the origin is
6x + 3y + z - 6 = 0
6x + 3y + 2z - 6= 0
6x + 3y + z + 6 = 0
6x + 3y + 2z + 6 = 0
The projection of a line segment on the axes are 9, 12 and 8. Then, the length of the line segment is
15
16
17
18
