 Multiple Choice Questions
Multiple Choice QuestionsThe equation of the plane through the line of intersection of the planes x - y + z + 3 = 0 and x + y + 22 + 1 = 0 and parallel to x-axis is
2y - z = 2
2y + z = 2
4y + z = 4
y - 2z = 3
The point of intersection of the straight line with the plane x + 3y - z + 1 = 0 is
(3, - 1, 1)
(- 5, 1, - 1)
(2, 0, 3)
(4, - 2, - 1)
The point P(x, y, z) lies in the first octant and its distance from the origin is 12 units. If the position vector of P make 45° and 60° with the x-axis and y-axis respectively, then the coordinates of P are
The distance between the planes r . (i + 2j - 2k) + 5 = 0 and r . (2i + 4j - 4k) - 16 = 0 is
3
13
If the angle between the line and the plane 2x - y + z + 4 = 0 is such that , then the value of p is
0
The ratio in which the plane y - 1 = 0 divides the straight line joining (1, - 1, 3) and (- 2, 5, 4) is
1 : 2
3 : 1
5 : 2
1 : 3
A.
1 : 2
Let the required ratio is
By section formula,
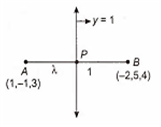
which lies on the line y = 1
which is the required ratio.
Equation of the line passing through i + j - 3k and perpendicular to the plane 2x - 4y + 3z + 5 = 0 is
The angle between the straight lines and x = 3r + 2; y = - 2r - 1; z = 2, where r is a parameter, is
