 Multiple Choice Questions
Multiple Choice QuestionsThe plane x + 3y + 13 = 0 passes through the line of intersection of the planes 2x - 8y + 4z = p and 3x - 5y + 4z + 10 = 0. If the plane is perpendicular to the plane 3x - y - 2z - 4 = 0, then the value of p is
2
5
9
3
If a straight line makes the angles 60°, 45° and with X, Y and Z-axes respectively, then is equal to
1
The direction cosines of the straight line given by the planes x = 0 and z = 0 are
1, 0, 0
0, 0, 1
1, 1, 0
0, 1, 0
The equation of the plane passing through (- 1, 5, - 7) and parallel to the plane 2x - 5y + 7z + 11 = 0, is
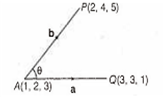
The angle subtended at the point (1, 2, 3) by the points P(2, 4, 5) and Q(3, 3, 1) is
90°
60°
30°
0°
A.
90°
Given, points
A(1, 2, 3), P(2, 4, 5) and 0(3, 3, 1).
If the line meets the plane x + 2y + 3z = 14 at P, then the distance between P and the origin is
