 Multiple Choice Questions
Multiple Choice QuestionsA circular wire of radius 7 cm is cut and bend again into an arc of a circle of radius 12 cm. Then angle subtended by the arc at the centre is:
50°
210°
100°
60°
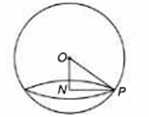
The radius of the circle x2 + y2 + z2 - 2y - 4z - 11 = 0 and x + 2y + 2z - 15 = 0 is :
3
C.
Since, the centre of sphere x2 + y2 + z2 - 2y - 4z - 11 = 0 is (0, 1, 2) and radius is 4.
Distance of a plane x + 2y + 2z - 15 = 0 from (0, 1, 2)
The points A (4, 5, 1), B (0, - 1, - 1), C(3, 9, 4) and D(- 4, 4, 4) are
collinear
coplanar
non-coplanar
non-collinear
The shortest distance from the point (1, 2, - 1) to the surface of the sphere x2 + y2 + z2 = 24 is :
unit
unit
2 sq unit
The equation of the plane which bisects the line joining (2, 3, 4) and (6, 7, 8) is :
x - y - z - 15 = 0
x - y - z - 15 = 0
x + y + z - 15 = 0
x + y + z + 15 = 0
The equation of the plane through the point (1, 2, 3), (- 1, 4, 2) and (3, 1, 1) is :
5x + y + 12z - 23 = 0
5x + 6y + 2z - 23 = 0
x + 6y + 2z - 13 = 0
x + y + z - 13 = 0
