The equation of the plane through (- 1, 1, 2) whose normal makes equal acute angles with coordinate axes is

• $\mathrm{r}. \left(\hat{\mathrm{i}} + \hat{\mathrm{j}} + \hat{\mathrm{k}}\right) = 2$

• $\mathrm{r}. \left(\hat{\mathrm{i}} + \hat{\mathrm{j}} + \hat{\mathrm{k}}\right) = 6$

• $\mathrm{r}. \left(3\hat{\mathrm{i}} - 3\hat{\mathrm{j}} + 3\hat{\mathrm{k}}\right) = 2$

• $\mathrm{r}. \left(\hat{\mathrm{i}} - \hat{\mathrm{j}} + \hat{\mathrm{k}}\right) = 3$

If distance of points $2\hat{\mathrm{i}} + 3\hat{\mathrm{j}} + \mathrm{\lambda }\hat{\mathrm{k}}$ from the plane $\mathrm{r} . \left(3\hat{\mathrm{i}} + 2\hat{\mathrm{j}} + 6\hat{\mathrm{k}}\right)$= 13 is 5 units, then $\mathrm{\lambda }$ = n

• $6, - \frac{17}{3}$

• $6, \frac{17}{3}$

• $- 6, - \frac{17}{3}$

• $- 6, \frac{17}{3}$

$∆$ABC has vertices at A = (2, 3, 5), B = (-1, 3, 2) and C = $\left(\mathrm{\lambda }, 5, \mathrm{\mu }\right)$. If the median through A is equally inclined to the axes, then the values of $\mathrm{\lambda } \mathrm{and} \mathrm{\mu }$ respectively are

• 10, 7

• 9, 10

• 7, 9

• 7, 10

264.

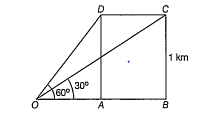
A plane is flying horizontally at a height of 1 km from ground. Angle of elevation of the plane at a certain instant is 60°. After 20 s, angle of elevation is found 30°. The speed of plane is

• $100\sqrt{3} \mathrm{m}/\mathrm{s}$

• $200\sqrt{3} \mathrm{m}/\mathrm{s}$

• $\frac{100}{\sqrt{3}} \mathrm{m}/\mathrm{s}$

• $\frac{200}{\sqrt{3}} \mathrm{m}/\mathrm{s}$

The maximum horizontal range of a ball projected with a velocity of 40 m/s is (take g = 9.8m/s²)

• 157 m

• 127 m

• 163 m

• 153 m

A body of 6 kg rests in limiting equilibrium on an inclined plane whose slope is 30°. If the plane is raised to slope of 60°, then force (in kg-wt) along the plane required to support it is

• 3

• $2\sqrt{3}$

• $\sqrt{3}$

• $3\sqrt{3}$

A gun projects a ball at the angle of 45° with the horizontal. If the horizontal range is 39.2 m, then the ball will rise to

• 9.8 m

• 4.9 m

• 2.45 m

• 19.6 m

The angle between two diagonals of a cube will be

• ${\sin }^{-1}\left(\frac{1}{3}\right)$

• ${\cos }^{-1}\left(\frac{1}{3}\right)$

• variable

• None of these

The lines $\frac{\mathrm{x} - \mathrm{a} + \mathrm{d}}{\mathrm{\alpha } - \mathrm{\delta }} = \frac{\mathrm{y} - \mathrm{a}}{\mathrm{\alpha }} = \frac{\mathrm{z} - \mathrm{a} - \mathrm{d}}{\mathrm{\alpha } + \mathrm{\delta }}$ and $\frac{\mathrm{x} - \mathrm{b} + \mathrm{c}}{\mathrm{\beta } - \mathrm{\tau }} = \frac{\mathrm{y} - \mathrm{b}}{\mathrm{\beta }} = \frac{\mathrm{z} - \mathrm{b} - \mathrm{c}}{\mathrm{\beta } + \mathrm{\tau }}$ are coplanar and then equation to the plane in which they lie, is

• x + y + z = 0

• x - y + z = 0

• x - 2y + z = 0

• x + y - 2z = 0

Two parallel unlike forces of magnitudes 15N and 10N are acting at points A and B respectively. If C is the point of action of resultant, then AB/BC is

• 2/1

• 1/2

• 2/3

• 3/2