 Multiple Choice Questions
Multiple Choice QuestionsThe distance of the point (- 2, 4, - 5) from the line is
A.
The line passes through A(- 3, 4, - 8) and is parallel to the vector b =
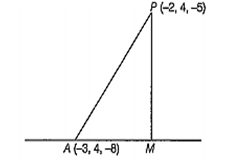
Let M be the foot of the perpendicular from P(- 2, 4, - 5) on the given line.
We, have
Clearly, AM = Projection of AP on b
If the equation of the locus of a point equidistant from the points (a1, b1) and (a2, b2) is (a1 - a2)r + (b1 - b2)y + c = 0, then the value of 'c' is
A tetrahedron has vertices at 0(0, 0, 0), A(1, 2, 1), B(2, 1, 3) and C(- 1, 1, 2). Then, the angle between the faces OAB and ABC will be
Given two vectors , the unit vector coplanar with the two vectors and perpendicular to first, is
None of these
If and vectors (1, a, a2), (1, b, b2) and (1, c, c2) are non-coplanar, then the product abc equals
2
- 1
1
0
If the length of perpendicular drawn from origin on a plane is 7 unit and its direction ratios are - 3, 2 and 6, then that plane is
- 3x + 2y + 6z - 7 = 0
- 3x + 2y + 6z - 49 = 0
3x - 2y + 6z + 7 = 0
- 3x + 2y - 6z - 49 = 0
