 Multiple Choice Questions
Multiple Choice QuestionsThe cosine of the angle between any two diagonals of a cube is
A.
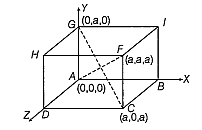
Direction ratios of AF = (a, a, a)
Direction ratios of CG = (a, - a, a)
Angle between diagonals CG and AF is
If the foot of the perpendicular from (0, 0, 0) to the plane is (1, 2, 2), then the equation ofthe plane is
- x + 2y + 8z - 9 = 0
x + 2y + 2z - 9 = 0
x + y + z - 5 = 0
x + 2y - 3z + 1 = 0
A variable plane is at a constant distance h from the origin and meets the coordinate axes in A, B, C. Locus of centroid of ABC is
x2 + y2 + z2 = h- 2
x2 + y2 + z2 = 4h- 2
x2 + y2 + z2 = 16h2
The direction ratios of normal to the plane passing through (0, 0, 1), (0, 1, 2) and (1, 0, 3) are
(2, 1, - 1)
(1, 0, 1)
(0, 0, - 1)
(1, 0, 0)
