$\mathrm{If} 3\hat{\mathrm{i}} + 3\hat{\mathrm{j}} + \sqrt{3}\hat{\mathrm{k}}, \sqrt{3}\hat{\mathrm{i}} + \sqrt{3}\hat{\mathrm{j}} + \mathrm{\lambda }\hat{\mathrm{k}} \mathrm{are} \mathrm{coplaner}, \mathrm{then} \mathrm{\lambda } \mathrm{is} \mathrm{equal} \mathrm{to}$

• 1

• 2

• 3

• 4

If the direction ratio of two lines are given by l + m + n = 0, mn - 2ln + lm = 0, then the angle between the lines is

• $\frac{\mathrm{\pi }}{4}$

• $\frac{\mathrm{\pi }}{3}$

• $\frac{\mathrm{\pi }}{2}$

• 0

If (2, - 1, 3) is the foot of the perpendicular drawn from the origin to the plane, then the equation of the plane is

• 2x + y - 3z + 6 = 0

• 2x - y + 3z - 14 = 0

• 2x - y + 3z - 13 = 0

• 2x + y + 3z - 10 = 0

If the plane 3x - 2y - z - 18 = 0 meets the coordinate axes in A, B, C then the centroid of $∆\mathrm{ABC}$ is

• (2, 3, - 6)

• (2, - 3, 6)

• (- 2, - 3, 6)

• (2, - 3, - 6)

The direction cosines of the line passing through P(2, 3, - 1) and the origin are

• $\frac{2}{\sqrt{14}}, \frac{{\displaystyle 3}}{{\displaystyle \sqrt{14}}}, \frac{{\displaystyle 1}}{{\displaystyle \sqrt{14}}}$

• $\frac{2}{\sqrt{14}}, \frac{{\displaystyle - 3}}{{\displaystyle \sqrt{14}}}, \frac{{\displaystyle 1}}{{\displaystyle \sqrt{14}}}$

• $\frac{- 2}{\sqrt{14}}, \frac{{\displaystyle - 3}}{{\displaystyle \sqrt{14}}}, \frac{{\displaystyle 1}}{{\displaystyle \sqrt{14}}}$

• $\frac{ 2}{\sqrt{14}}, \frac{{\displaystyle - 3}}{{\displaystyle \sqrt{14}}}, \frac{{\displaystyle - 1}}{{\displaystyle \sqrt{14}}}$

If the direction cosines of two lines are such that l + m + n = 0, l² + m² - n² = 0, then the angle between them is :

• $\mathrm{\pi }$

• $\frac{\mathrm{\pi }}{3}$

• $\frac{\mathrm{\pi }}{4}$

• $\frac{\mathrm{\pi }}{6}$

The ratio in which yz-plane divides the line segment joining ( - 3, 4, - 2) and (2, 1, 3) is

• - 4 : 1

• 3 : 2

• - 2 : 3

• 1 :4

The cosine of the angle A of the tnangle with vertices

A(1, - 1, 2), B(6, 11, 2), C(1, 2, 6) is

• $\raisebox{1ex}{$63$}\!\left/ \!\raisebox{-1ex}{$65$}\right.$

• $\raisebox{1ex}{$36$}\!\left/ \!\raisebox{-1ex}{$65$}\right.$

• $\raisebox{1ex}{${\displaystyle 16}$}\!\left/ \!\raisebox{-1ex}{${\displaystyle 65}$}\right.$

• $\raisebox{1ex}{$13$}\!\left/ \!\raisebox{-1ex}{$64$}\right.$

The angle between the lines whose direction 

cosine are $\left(\frac{\sqrt{3}}{4}, \frac{1}{4}, \frac{\sqrt{3}}{2}\right) \mathrm{and} \left(\frac{\sqrt{3}}{4}, \frac{1}{4}, \frac{- \sqrt{3}}{2}\right), \mathrm{is}$

• $\mathrm{\pi }$

• $\frac{\mathrm{\pi }}{2}$

• $\frac{\mathrm{\pi }}{3}$

• $\frac{\mathrm{\pi }}{4}$

410.

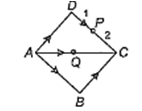
In a quadrilateral ABCD, the point P divides DC in the ratio 1 : 2 and Q is the mid point of AC. If$\overrightarrow{\mathrm{AB}} + 2\overrightarrow{\mathrm{AD}} + \overrightarrow{\mathrm{BC}} - 2\overrightarrow{\mathrm{DC}} = \mathrm{k}\overrightarrow{\mathrm{PQ}},$ then k is equal

• - 6

• - 4

• 6

• 4