A girl walks 4 km towards West, then she walks 3 km in a drection 30° East of North and stops. Then, the girl's displacement from herinitial point of departures is

• $- \frac{5}{2}\hat{\mathrm{i}} + \frac{3\sqrt{3}}{2}\hat{\mathrm{j}}$

• $\frac{1}{2}\hat{\mathrm{i}} + \frac{\sqrt{3}}{2}\hat{\mathrm{j}}$

• $- \frac{1}{2}\hat{\mathrm{i}} + \frac{3\sqrt{3}}{2}\hat{\mathrm{j}}$

• None of these

If a = $\hat{\mathrm{i}} + \hat{\mathrm{j}} + \hat{\mathrm{k}}$,b = $4\hat{\mathrm{i}} + 3\hat{\mathrm{j}} + 4\hat{\mathrm{k}}$ and c = $\hat{\mathrm{i}} + \mathrm{\alpha }\hat{\mathrm{j}} + \mathrm{\beta }\hat{\mathrm{k}}$ are linearly dependent vectors and $\left|\mathrm{c}\right| = \sqrt{3}$, then the value of $\mathrm{\alpha } \mathrm{and} \mathrm{\beta }$ are respectively

• $\pm 1, 1$

• $\pm 2, 1$

• $0, \pm 1$

• None of these

The projection of the vector a = $\hat{\mathrm{i}} - 2\hat{\mathrm{j}} + \hat{\mathrm{k}}$ on  the vextor $\mathrm{b} = 4\hat{\mathrm{i}} - 4\hat{\mathrm{j}} + 7\hat{\mathrm{k}}$ is

• $\frac{9}{19}$

• $\frac{19}{9}$

• 9

• $\sqrt{19}$

Forces of magnitude 5 and 3 units acting in the directions $6\hat{\mathrm{i}} + 2\hat{\mathrm{j}} +\hspace{0.17em}3\hat{\mathrm{k}}$ and $3\hat{\mathrm{i}} - 2\hat{\mathrm{j}} +\hspace{0.17em}6\hat{\mathrm{k}}$ respectively act on a particle which is displaced from the point (2, 2, - 1) to (4, 3, 1). The work done by the forces is

• 148 units

• $\frac{148}{7} \mathrm{units}$

• $\frac{78}{7} \mathrm{units}$

• None of these

If a and b are unit vectors and $\mathrm{\theta }$ is the angle between them, then la + bl < 1, if

• $\mathrm{\theta } = \frac{\mathrm{\pi }}{2}$

• $\mathrm{\theta } < \frac{\mathrm{\pi }}{3}$

• $\mathrm{\pi } \ge \mathrm{\theta } > \frac{2\mathrm{\pi }}{3}$

• $\frac{\mathrm{\pi }}{3} < \mathrm{\theta } < \frac{2\mathrm{\pi }}{3}$

The points, whose position vectors are 60i + 3j, 40i - 8j and ai - 52j collinear, if

• a = 40

• a = - 40

• a = 20

• a = - 20

In a $∆$ABC, AB = ri + j, AC = si - j if the area of triangle is of unit magnitude, then

• $\left|\mathrm{r} - \mathrm{s}\right| = 2$

• $\left|\mathrm{r} + \mathrm{s}\right| = 1$

• $\left|\mathrm{r} + \mathrm{s}\right| = 2$

• $\left|\mathrm{r} - \mathrm{s}\right| = 1$

If a = i - j + k, a b = 0, a x b = c, where c = - 2i - j + k, then b 1s equal to

• (1, 0, - 1)

• (0, 1, 1)

• (- 1, - 1, 0)

• (- 1, 0, 1)

The resultant of P and Q is R. If Q is doubled, R is also doubled and if Q is reversed, R is again doubled. Then, P² : Q² : R² gven by

• 2 2 3

• 3 2 2

• 2 3 2

• 2 3 1

230.

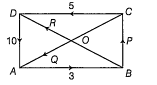
Forces ofmagnitudes 3, P, 5, 10 and Q are respectively acting along the sides AB, BC, CD, AD and the diagonal CA of a rectangle ABCD, where AB = 4m and BC = 3m. Ifthe resultant is a single force along the other diagonal BD, then P, Q and the resultant are

• $4, 10\frac{5}{12}, 12\frac{11}{12}$

• 5, 6, 7

• $3\frac{1}{2}, 8, 9\frac{1}{2}$

• None of the above