Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Vector Algebra

Multiple Choice Questions

431.

$The volume (in cubic units) of the tetrahedron with edges \hat{i} + \hat{j} + \hat{k}, \hat{i} - \hat{j} + \hat{k} and \hat{i} + 2 \hat{j} - \hat{k} is$

4
$\frac{2}{3}$
$\frac{1}{6}$
$\frac{1}{3}$

432.

$Let \vec{a} = a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k} Assertion (A) : The identity {|\vec{a} \times \hat{i}|}^{2} + {|\vec{a} \times \hat{j}|}^{2} + {|\vec{a} \times \hat{k}|}^{2} = 2 {|\vec{a}|}^{2} holds for \vec{a} Reason (R) : \vec{a} \times \hat{i} = a_{3} \hat{j} - a_{2} \hat{k}, \vec{a} \times \hat{j} = a_{1} \hat{k} - a_{3} \hat{i}, \vec{a} \times \hat{k} = a_{2} \hat{i} - a_{1} \hat{j} Wich of the following is correct ?$

Both (A) and (R) are true and (R) is the correct reason for (A)
Both (A) and (R) are true but (R) is not the correct reason for (A)
(A) is true, (R) is false
A) is false, (R) is true

433.

The position vectors of P and Q are $\vec{a} and \vec{b}$ respectively. If R is a point on PQ such that $\vec{PR} = 5 \vec{PQ}$ , then the position vector of R is

$5 \vec{b} - 4 \vec{a}$
$5 \vec{b} + 4 \vec{a}$
$4 \vec{b} - 5 \vec{a}$
$4 \vec{b} + 5 \vec{a}$

434.

If the points with position vectors $60 \hat{i} + 3 \hat{j}, 40 \hat{i} - 8 \hat{j} and a \hat{i} - 52 \hat{j} are collinear, then a is equal to$ are collinear,then a is equal to

- 40
- 20
20
40

435.

If the position vectors of A, B and C are respectively $2 \hat{I} - \hat{J} + \hat{K}, \hat{I} - 3 \hat{J} - 5 \hat{K} and 3 \hat{i} - 4 \hat{j} - 4 \hat{k}, then \cos^{2} (A) = ?$

0
$\frac{6}{41}$
$\frac{35}{41}$
1

436.

$Let \vec{a} be a unit vector, \vec{b} = 2 \hat{i} + \hat{j} - \hat{k} and \vec{c} = \hat{i} + 3 \hat{k} . Then, maximum value of [\vec{a} \vec{b} \vec{c}] is$

- 1
$\sqrt{10} + \sqrt{6}$
$\sqrt{10} - \sqrt{6}$
$\sqrt{59}$

Match The Following

437.

If $\vec{a} = \hat{i} + \hat{j} + \hat{k}, \vec{b} = \hat{i} - \hat{j} + \hat{k}, \vec{c} = \hat{i} + \hat{j} - \hat{k}$ and $\vec{d} = \hat{i} - \hat{j} - \hat{k}$ , then observe the following lists

List-I List-II

(i) $\vec{a} . \vec{b}$ (A) $\vec{a} . \vec{d}$

(ii) $\vec{b} . \vec{c}$ (B) 3

(iii) $[\vec{a} \vec{b} \vec{c}]$ (C) $\vec{b} . \vec{d}$

(iv) $\vec{b} \times \vec{c}$ (D) $2 \hat{i} - \hat{k}$

(E) $2 \hat{j} + 2 \hat{k}$

(F) 4

Then, correct match of List_I to List-II is

A. (i) (ii) (iii) (iv)	(i) C A B F
B. (i) (ii) (iii) (iv)	(ii) C A F E
C. (i) (ii) (iii) (iv)	(iii) A C B F
D. (i) (ii) (iii) (iv)	(iv) A C F D

Multiple Choice Questions

438.

$If m_{1}, m_{2}, m_{3} and m_{4} are respectively the magnitudes of the vectors {\vec{a}}_{1} = 2 \hat{i} - \hat{j} + \hat{k}, {\vec{a}}_{2} = 3 \hat{i} - 4 \hat{j} - 4 \hat{k}, {\vec{a}}_{3} = \hat{i} + \hat{j} - \hat{k} and {\vec{a}}_{4} = - \hat{i} + 3 \hat{j} + \hat{k}, then the correct order of m_{1}, m_{2}, m_{3} and m_{4} is$

$m_{3} < m_{1} < m_{4} < m_{2}$
$m_{3} < m_{1} < m_{2} < m_{4}$
$m_{3} < m_{4} < m_{1} < m_{2}$
$m_{3} < m_{4} < m_{2} < m_{1}$

439.
$Let \vec{a} = \hat{i} - 2 \hat{j} + 3 \hat{k}, \vec{b} = 2 \hat{i} + 3 \hat{j} - \hat{k}, \vec{c} = \hat{i} - 2 \hat{j} + 3 \hat{k}$ . If $\vec{c}$ is parallel to the plane containing $\vec{a}, \vec{b}$ , then $λ$ is equal to

0

1

- 1

2

$Given that, \vec{a} = \hat{i} - 2 \hat{j} + 3 \hat{k}, \vec{b} = 2 \hat{i} + 3 \hat{j} - \hat{k}, \vec{c} = \hat{i} - 2 \hat{j} + 3 \hat{k}$

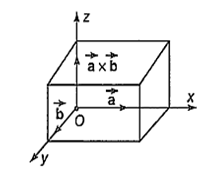
Also, since $\vec{a} and \vec{b}$ lies in the same plane, then $(\vec{a} \times \vec{b})$ is perpendicular vector to this plane. Given that vector $\vec{c}$ is parallel to the plane containing $\vec{a} and \vec{b}$ , so vector $(\vec{a} \times \vec{b})$ also perpendicular to the vector $\vec{c} i . e ., (θ = 90 °)$ . So, $(\vec{a} \times \vec{b}) \vec{c}$ should be equal to zero

or $(\vec{a} \times \vec{b}) \vec{c}$ = 0 ...(i)

$\vec{a} \times \vec{b} = |\begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & - 2 & 3 \\ 2 & 3 & - 1 \end{matrix}| = (2 - 9) \hat{i} + (6 + 1) \hat{j} + (3 + 4) \hat{k} = - 7 \hat{i} + 7 \hat{j} + 7 k$

Then, from Eq. (i)

$(- 7 \hat{i} + 7 \hat{j} + 7 \hat{k}) (λ \hat{i} + \hat{j} + (2 λ - 1) \hat{k}) = 0 \Rightarrow - 7 λ + 7 + 7 (2 λ - 1) = 0$

$\Rightarrow - 7 λ + 7 + 14 λ - 7 = 0 \Rightarrow 7 λ = 0 \Rightarrow λ = 0 Hence, the value of λis 0 .$

440.

If three unit vectors $\vec{a}, \vec{b}, \vec{c}$ satisfy $\vec{a} + \vec{b} + \vec{c}$ , then the angle between a and b is

$\frac{2 π}{3}$
$\frac{5 π}{6}$
$\frac{π}{3}$
$\frac{π}{6}$

	List-I		List-II
(i)	$\vec{a} . \vec{b}$	(A)	$\vec{a} . \vec{d}$
(ii)	$\vec{b} . \vec{c}$	(B)	3
(iii)	$[\vec{a} \vec{b} \vec{c}]$	(C)	$\vec{b} . \vec{d}$
(iv)	$\vec{b} \times \vec{c}$	(D)	$2 \hat{i} - \hat{k}$
		(E)	$2 \hat{j} + 2 \hat{k}$
		(F)	4

Previous Year Papers

Test Series

Test Yourself

Multiple Choice Questions

Match The Following

Multiple Choice Questions

439. Let a→ = i^ - 2j^ + 3k^, b→ = 2i^ + 3j^ - k^, c→ = i^ - 2j^ + 3k^. If c→ is parallel to the plane containing a→, b→, then λ is equal to 0 1 - 1 2

439.
$Let \vec{a} = \hat{i} - 2 \hat{j} + 3 \hat{k}, \vec{b} = 2 \hat{i} + 3 \hat{j} - \hat{k}, \vec{c} = \hat{i} - 2 \hat{j} + 3 \hat{k}$ . If $\vec{c}$ is parallel to the plane containing $\vec{a}, \vec{b}$ , then $λ$ is equal to

0

1

- 1

2