Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

101.
Two spheres of electric charges + 2 nC and −8 nC are placed at a distance d apart. If they are allowed to touch each other, what is the new distance between them to get a repulsive force of same magnitude as before ?

d

$\frac{d}{2}$

$\frac{3 d}{4}$

$\frac{4 d}{3}$

$\frac{3 d}{4}$

In the first condition,

Given,

$q_{1} = - 2 nC = 2 \times 10^{- 9} C q_{2} = - 8 nC = - 8 \times 10^{9} C F = \frac{{kq}_{1} q_{2}}{r^{2}} F = \frac{k (2 \times 10^{- 9}) \times (8 \times 10^{- 9})}{a^{2}} F = \frac{k (16 \times 10^{- 18})}{a^{2}} . . . . . . (i)$

In the second condition,

$F_{1} = \frac{{kq}_{1} q_{2}}{d'^{2}}$

After touching of sphere to each other the total charge = 2 − 8 = −6 nC

Charge on each sphere = 3 nC

= 3 × 10^-9 C

$F_{1} = \frac{k (3 \times 10^{- 9}) (3 \times 10^{- 9})}{{(d')}^{2}} F_{1} = \frac{k (9 \times 10^{- 18})}{{(d')}^{2}} . . . . . . (ii)$

From Eqs. (i) and (ii), we get

$\frac{k (16 \times 10^{- 18})}{d'^{2}} = \frac{k (9 \times 10^{- 18})}{{(d')}^{2}} \frac{d^{2}}{d'^{2}} = \frac{16 \times 10^{- 18}}{9 \times 10^{- 18}} \frac{d^{2}}{d'^{2}} = \frac{16}{9} \frac{d}{d'} = \sqrt{\frac{16}{9}} \frac{d}{d'} = \frac{4}{3} d = \frac{4}{3} d' d' = \frac{3}{4} d$

102.

Three point charges of + 2q, + 2q and − 4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is

2qx
$3 \sqrt{2} qx$
3qx
$2 \sqrt{3} qx$

103.

64 small drops of mercury, each of radius r and charge q coalesce to form a big drop. The ratio of the surface density of charge of each small drop with of the big drop is

64 : 1
1 : 64
1 : 4
4 : 1

104.

Three point charges are placed at the corners of an equilateral triangle. Assuming only electrostatic forces are acting. Then the system

will be in equilibrium if the charges rotate about the centre of the triangle
can never be in equilibrium
will be in equilibrium if the charges have the same magnitudes but different sign
will be in equilibrium if the charges have different magnitude and different signs.

105.

Two copper balls, each weighing 10 g are kept in air 10 cm apart. If one electron from every 10⁶ atoms is transferred from one ball to the other, the Coulomb force between them is (atomic weight of copperis 63.5)

2.0 × 10⁴ N
2.0 × 10¹⁰ N
2.0 × 10⁶ N
2.0 × 10⁶ N

106.

The electric field in a certain region is acting radially outward and is given by E = Ar. A charge contained in a sphere of radius 'a' centred at the origin of the field will be given by

$4 πε subscript straight o Aa squared$
$Aε subscript straight o straight a squared$
$4 πε subscript straight o Aa cubed$
$4 πε subscript straight o Aa cubed$

1875 Views

107.

In a coil of resistance 10Ω, the induced current developed by changing magnetic flux through it is shown in the figure as a function of time. The magnitude of change in flux through the coil in weber is

439 Views

108.

What is the flux through a cube of side a if a point charge of q is a one of its corner?

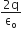
$fraction numerator 2 straight q over denominator straight epsilon subscript straight o end fraction$
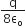
$fraction numerator straight q over denominator 8 straight epsilon subscript straight o end fraction$
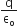
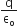
$straight q over straight epsilon subscript straight o$
$straight q over straight epsilon subscript straight o$

818 Views

109.

Two thin dielectric slabs of dielectric constants K₁ and K₂ (K₁ < K₂) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field E between the plates with distance d as measured from plate P is correctly shown by: