 Multiple Choice Questions
Multiple Choice QuestionsA satellite in a circular orbit of radius R has a period of 4 h. Another satellite with orbital radius 3 R around the same planet will have a period (in hours)
16
4
The acceleration due to gravity becomes (g = acceleration due to gravity on the surface of the earth) at a height equal to
4R
2R
A planet revolves around the sun in an elliptical orbit. The linear speed of the planet will be maximum at

D
B
A
C
An astronaut on a strange planet finds that acceleration due to gravity is twice as that on the surface of earth. Which of the following could explain this ?
Both the mass and radius of the planet are half as that of earth
Radius of the planet is half as that of earth, but the mass is the same as that of earth
Both the mass and radius of the planet are twice as that of earth
Mass of the planet is half as that of earth, but radius is same as that of earth
Two satellites of mass m and 9m are orbiting a planet in orbits of radius R. Their periods of revolution will be in the ratio of
9 : 1
3 : 1
1 : 1
1 : 3
Faintest stars are called
zero magnitude stars
second magnitude stars
sixth magnitude stars
dwarfs
A planet moving around sun sweeps area A1 in 2 days, A2 in 3 days and A3 in 6 days. Then, the relation between A1, A2 and A3 is

6A1 = 3A2 = 2A3
3A1 = 2A2 = A3
2A1 = 3A2 = 6A3
3A1 = 2A2 = 6A3
Earth is moving around the sun in elliptical orbit as shown. The ratio of OB and OA is R. Then the ratio of Earth's velocities at A and B is

R-1
R
R2/3
C.
R
In central force motion, the angular momentum of body remains conserved.
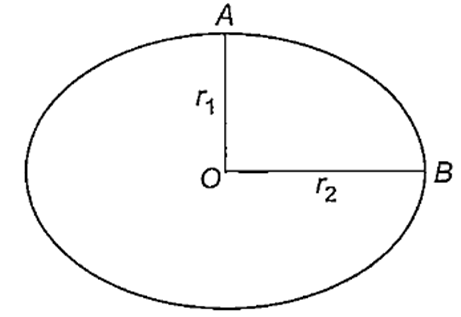
i.e, Angular momentum,
L = r × p = mvr
[at minor and major axis v and are perpendicular]
So, if v1 and v2 be the speed of earth at A and B, respectively
Then, mv1r1 = mv2r2
What is a period of revolution of the earth satellite ? Ignore the height of satellite above the surface of the earth. Given :
85 min
156 min
83.73 min
90 min
