 Multiple Choice Questions
Multiple Choice QuestionsA mass of diatomic gas  at a pressure of 2 atm is compressed adiabatically so that its temperature rise from 27oC to 927o C. The pressure of the gas is final state is
at a pressure of 2 atm is compressed adiabatically so that its temperature rise from 27oC to 927o C. The pressure of the gas is final state is
28 atm
68.7 atm
256 atm
256 atm
If ΔU and ΔW represent the increase in internal energy and work done by the system respectively in the thermodynamical process, which of the following is true?
ΔU = - ΔW, in a adiabatic process
ΔU = ΔW, in an isothermal process
ΔU = ΔW, in an adiabatic process
ΔU = ΔW, in an adiabatic process
A monatomic gas at pressure p1 and V1 is compressed adiabatically to 1/8 th its original volume. What is the final pressure of the gas?
64 p1
p1
16 p1
16 p1
The internal energy change in a system that has absorbed 2 Kcal of heat and done 500 J of work is
8900 J
6400 J
5400 J
5400 J
In a thermodynamic process which of the following statements is not true?
In an adiabatic process, the system is insulated from the surroundings
In an isochoric process pressure remains constant
In an isothermal process, the temperature remains constant
In an isothermal process, the temperature remains constant
If Q, E andW denote respectively the heat added, change in internal energy and the work done in a closed cycle process, then
W =0
Q = W = 0
E=0
E=0
In producing chlorine through electrolysis 100 W power at 125 V is being consumed. How much chlorine per min is liberated? ECE of chlorine is 0.367 x 10-6 kg/C
17.6 mg
21.3 mg
24.3 mg
24.3 mg
A Carnot engine whose sink is at 300 K has an efficiency of 40%. By how much should the temperature of source be increased so as to increase its efficiency by 50% of original efficiency?
275 K
175 K
250 K
250 K
The molar specific heat at constant pressure of an ideal gas is (7/2)R. The ratio of specific heat at constant pressure to that at constant volume is
7/5
8/7
5/7
5/7
A.
7/5
We have given molar specific heat at constant pressure
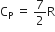
Mayor's relation can be written as:
Molar specific heat at constant volume = Gas constant
i.e., CP - CV = R

Hence, required ratio is

Two rods A and B of different materials are welded together as shown in the figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be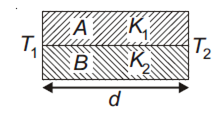
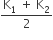
k1 + k2
k1 + k2
