 Multiple Choice Questions
Multiple Choice QuestionsIf E is the universal set and A = B C, then the set E - (E - (E - (E - (E - A)))) is same as the set :
If A = {x : x is a multiple of 2}, B = {x : x is a multiple of 5} and C = {x : x is a multiple of 10}, then is equal to :
A
B
C
{x : x is a multiple of 100}
Let S be a set of all distinct numbers of the form "q' where p. q { 1, 2, 3, 4, 5, 6}. What is the cardinality of the set S ?
21
23
32
36
B.
23
When p = 2, q = {1, 3, 5}
So, total elements in S in this case = 3
When p = 3, q = {1, 2, 4, 5}
So, total elements in S in this case = 4
When p = 4, q = {1, 3, 5}
So, total elements in S in this case = 3
When p = 5, q = {1, 2, ,3, 4, 5, 6}
So, total elements in S in this case = 5
When p = 6, q = {1, 5}
So, total elements in S in this case = 2
So, cardinality of set
S = 6 + 3 + 4 + 3 + 5 + 2 = 23
Let S = {2, 4, 6, 8, ..........20}. What is the maximum number of subsets does S have ?
10
20
512
1024
If a set A contains 3 elements and another set B contains 6 elements, then what is the minimum number of elements that (A U B) can have ?
3
6
8
9
If A, B and C are subsets of a given set, then which one of the following relations is not correct ?
A U (A ∩ B) = A U B
A ∩ (A U B) = A
(A ∩ B) U C = (A U C) ∩ (B U C)
(A U B) ∩ C = (A ∩ C) U (B ∩ C)
Consider the following Venn diagram, where X, Y and Z are three sets. Let the number of elements in z be denoted by n(Z) which is equal to 90
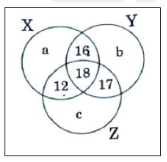
If the number of elements belonging to neither X, nor Y, nor Z is equal to p, then what is the number of elements in the complement of X ?
p + b + 60
p + b + 40
p + a + 60
p + a + 40
Consider the following Venn diagram, where X, Y and Z are three sets. Let the number of elements in z be denoted by n(Z) which is equal to 90
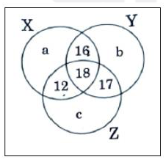
What is the value of n(X) + n(Y) + n(Z) – n(X ∩ Y) – n(Y ∩ Z) – n(X ∩ Z) + n(X ∩ Y ∩ Z) ?
a + b + 43
a + b + 63
a + b + 96
a + b + 106
