 Multiple Choice Questions
Multiple Choice QuestionsThe resistance of an ammeter is 13 Ω and its scale is graduated for a current upto 100 A. After an additional shunt has been connected to this ammeter it becomes possible to measure currents upto 750 A by this meter. The value of
shunt resistance is
20 Ω
2 Ω
0.2 Ω
2 KΩ
Three resistances P, Q, R each of 2Ω and an unknown resistance S form the four arms of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S?
2 Ω
3 Ω
6 Ω
1 Ω
For a metallic wire, the ratio ( V = applied potential difference and i = current flowing) is
independent of temperature
increases as the temperature rises
decreases as the temperature rises
increases or decreases as temperature rises depending upon the metal
A galvanometer having a resistance of 8 Ω is shunted by a wire of resistance 2 Ω.1f the total current is 1 A, the part of it passing through the shunt will be
0.25 A
0.8 A
0.2 A
0.5 A
B.
0.8 A
Potential difference across galvanometer should be equal to potential difference across shunt.
The shunt and galvanometer are connected as shown figure.

Let total current through the parallel combination is i, the current through the galvanometer is ig and the current through the shunt is ( i - ig )
The potential difference Vab ( = Va - Vb ) is the same for both paths, so
ig G = ( i - ig ) S
⇒ ig ( G + S ) = i S
![]()
The fraction of current passing through shunt:
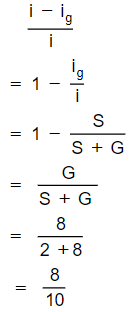
The fraction of current passing through shunt
= 0.8 A
At room temperature, copper has free electron density of 8.4 x 1028 m-3, The electron drift velocity in a copper conductor of cross-section area of 10-6 m2 and carrying a current of 5.4 A will be
4 ms-1
0.4 ms-1
4 ms-1
0.4 mm s-1
A uniform wire of resistance R and length L is cut into four equal parts, each of length L/4, which are then connected in parallel combination. The effective resistance of the combination will be
R
4 R
A capacitor of capacitance 5µF is connected as shown in the figure. The internal resistance of the cell is 0.5 Ω . The amount of charge on the capacitor plates is

80 μC
40 μC
20 μC
10 μC
A current of 5A is passing through a metalic wire of cross-sectional area 4 × 10-6 m2 . If the density of charge carriers of the wire is 5 × 1026 m-3, then the drift velocity of the electrons will be
1 × 102 m/s
1.56 × 10-2 m /s
1.56 × 10-3 m/s
1 × 10-2 m/s
